Chuyên đề 3. HÀM SỐ LƯỢNG GIÁC VÀ ĐỒ THỊ
Dạng 1. Tìm tập xác định của hàm số
Phương pháp giải
Bài tập 1
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{\tan 2x}{\cos x+1}+\sin x\).
Điều kiện:
\(\begin{cases}\cos x+1\neq 0\\ \cos 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases}\cos x\neq -1\\ \cos 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq \pi +k2\pi\\2x\neq \displaystyle\frac{\pi}{2}+k\pi\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq \pi +k2\pi\\x\neq \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2}.\end{cases}\)
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace\pi +k2\pi;\, \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2},\, k\in \mathbb{Z} \right\rbrace\).
Bài tập 2
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{\cos 3x}{1-\sin x}+\tan x\).
Điều kiện:
\(\begin{cases}1-\sin x\neq 0\\ \cos x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases}\sin x\neq 1\\ \cos x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq \displaystyle\frac{\pi}{2} +k2\pi\\x\neq \displaystyle\frac{\pi}{2}+k\pi\end{cases}\) \(\Leftrightarrow x\neq \displaystyle\frac{\pi}{2}+k\pi\).
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace \displaystyle\frac{\pi}{2}+k\pi,\, k\in \mathbb{Z} \right\rbrace\).
Bài tập 3
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{2\tan 2x-5}{\sin 2x+1}\).
Điều kiện:
\(\begin{cases}\sin 2x+1\neq 0\\ \cos 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases}\sin 2x\neq -1\\ \cos 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} 2x\neq -\displaystyle\frac{\pi}{2} +k2\pi\\2x\neq \displaystyle\frac{\pi}{2}+k\pi\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq -\displaystyle\frac{\pi}{4} +k\pi\\x\neq \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2}\end{cases}\) \(\Leftrightarrow x\neq \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2}, \, k\in \mathbb{Z} \right\rbrace\).
Bài tập 4
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{1}{\tan x-1}\).
Điều kiện:
\(\begin{cases}\tan x-1\neq 0\\ \cos x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases}\tan x\neq 1\\ \cos x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq \displaystyle\frac{\pi}{4} +k\pi\\x\neq \displaystyle\frac{\pi}{2}+k\pi.\end{cases}\)
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace\displaystyle\frac{\pi}{4} +k\pi;\, \displaystyle\frac{\pi}{2}+k\pi,\, k\in \mathbb{Z} \right\rbrace\).
Bài tập 5
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{3}{\cos^2 x-\sin^2 x}+\tan x\).
Ta có \(y=\displaystyle\frac{3}{\cos^2 x-\sin^2 x}+\tan x=\displaystyle\frac{3}{\cos 2x}+\tan x\).
Điều kiện:
\(\begin{cases}\cos x\neq 0\\ \cos 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq \displaystyle\frac{\pi}{2} +k\pi\\2x\neq \displaystyle\frac{\pi}{2}+k\pi\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq \displaystyle\frac{\pi}{2} +k\pi\\x\neq \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2}.\end{cases}\)
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace\displaystyle\frac{\pi}{2} +k\pi;\, \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2},\, k\in \mathbb{Z} \right\rbrace\).
Bài tập 6
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{1}{\sin x}+\displaystyle\frac{1}{\cos x}\).
Điều kiện:
\(\begin{cases}\cos x\neq 0\\ \sin x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq k\pi\\x\neq \displaystyle\frac{\pi}{2}+k\pi\end{cases}\) \(\Leftrightarrow x\neq k\displaystyle\frac{\pi}{2}.\)
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace k\displaystyle\frac{\pi}{2},\, k\in \mathbb{Z} \right\rbrace\).
Bài tập 7
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\sqrt{\displaystyle\frac{2-\sin x}{\cos x+1}}\).
Điều kiện: \(\displaystyle\frac{2-\sin x}{\cos x+1}\geq 0\).
Với mọi \(x\in \mathbb{R}\), ta có
\(-1\leq \sin x\leq 1\Leftrightarrow 1\leq 2-\sin x\leq 3;\)
\(-1\leq \cos x\leq 1\Leftrightarrow 0\leq \cos x+1\leq 2.\)
Do đó
\(\displaystyle\frac{2-\sin x}{\cos x+1}\geq 0\Leftrightarrow \cos x+1\neq 0\) \(\Leftrightarrow \cos x\neq -1\Leftrightarrow x\neq \pi +k2\pi.\)
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace \pi +k2\pi, \, k\in \mathbb{Z} \right\rbrace\).
Bài tập 8
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{1}{\sqrt{1-\sin x}}\).
Điều kiện:
\(1-\sin x> 0\Leftrightarrow \sin x<1\) \(\Leftrightarrow \sin x \neq 1\Leftrightarrow x \neq \displaystyle\frac{\pi}{2}+k2\pi\).
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace \displaystyle\frac{\pi}{2}+k2\pi, \, k\in \mathbb{Z} \right\rbrace\).
Bài tập 9
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\sqrt{\displaystyle\frac{\cos x+4}{\sin x+1}}\).
Điều kiện: \(\displaystyle\frac{\cos x+4}{\sin x+1}\geq 0\).
Với mọi \(x\in \mathbb{R}\), ta có
\(-1\leq \sin x\leq 1\Leftrightarrow 0\leq \sin x+1\leq 2;\)
\(-1\leq \cos x\leq 1\Leftrightarrow 3\leq \cos x+4\leq 5.\)
Do đó
\(\displaystyle\frac{\cos x+4}{\sin x+1}\geq 0\Leftrightarrow \sin x+1\neq 0\) \(\Leftrightarrow \sin x\neq -1\Leftrightarrow x\neq -\displaystyle\frac{\pi}{2} +k2\pi\).
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace -\displaystyle\frac{\pi}{2} +k2\pi, \, k\in \mathbb{Z} \right\rbrace\).
Bài tập 10
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\sqrt{\displaystyle\frac{2-\cos x}{1-\sin x}}\).
Điều kiện: \(\displaystyle\frac{2-\cos x}{1-\sin x}\geq 0\).
Với mọi \(x\in \mathbb{R}\), ta có
\(-1\leq \sin x\leq 1\Leftrightarrow 0\leq 1-\sin x\leq 2;\)
\(-1\leq \cos x\leq 1\Leftrightarrow 1\leq 2-\cos x\leq 3.\)
Do đó
\(\displaystyle\frac{2-\cos x}{1-\sin x}\geq 0\Leftrightarrow 1-\sin x\neq 0 \Leftrightarrow \sin x\neq 1\Leftrightarrow x\neq \displaystyle\frac{\pi}{2} +k2\pi\).
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace \displaystyle\frac{\pi}{2} +k2\pi, \, k\in \mathbb{Z} \right\rbrace\).
Bài tập 11
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\sqrt{4\pi^2-x^2}+\cot 2x\).
Điều kiện:
\(\begin{cases} 4\pi^2-x^2\geq 0\\\sin 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases}-2\pi\leq x\leq 2\pi\\2x\neq k\pi\end{cases}\) \(\Leftrightarrow \begin{cases}-2\pi\leq x\leq 2\pi\\x\neq k\displaystyle\frac{\pi}{2}.\end{cases}\)
Ta có
\(-2\pi\leq k\displaystyle\frac{\pi}{2}\leq 2\pi\Leftrightarrow -4\leq k\leq 4\).
Tập xác định \(\mathscr{D}=(-2\pi;2\pi)\setminus\left\lbrace \pm \displaystyle\frac{3\pi}{2};\pm \pi; \pm\displaystyle\frac{\pi}{2};0 \right\rbrace\).
Bài tập 12
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\sqrt{\pi^2-x^2}+\cot 2x\).
Điều kiện:
\(\begin{cases} \pi^2-x^2\geq 0\\\sin 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases}-\pi\leq x\leq \pi\\2x\neq k\pi\end{cases}\) \(\Leftrightarrow \begin{cases}-\pi\leq x\leq \pi\\x\neq k\displaystyle\frac{\pi}{2}.\end{cases}\)
Ta có \(-\pi\leq k\displaystyle\frac{\pi}{2}\leq \pi\Leftrightarrow -2\leq k\leq 2\).
Tập xác định \(\mathscr{D}=(-\pi;\pi)\setminus\left\lbrace\pm\displaystyle\frac{\pi}{2};0 \right\rbrace\).
Bài tập 13
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{\sqrt{\pi^2-x^2}}{\sin 2x+1}\).
Điều kiện: \(\begin{cases} \pi^2-x^2\geq 0\\\sin 2x+1\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} \pi^2-x^2\geq 0\\\sin 2x\neq -1\end{cases}\) \(\Leftrightarrow \begin{cases}-\pi\leq x\leq \pi\\2x\neq -\displaystyle\frac{\pi}{2}+ k2\pi\end{cases}\) \(\Leftrightarrow \begin{cases}-\pi\leq x\leq \pi\\x\neq -\displaystyle\frac{\pi}{4}+k\pi.\end{cases}\)
Ta có
\(-\pi\leq -\displaystyle\frac{\pi}{4}+k\pi\leq \pi\) \(\Leftrightarrow -\displaystyle\frac{3}{4}\leq k\leq \displaystyle\frac{5}{4}\).
Tập xác định \(\mathscr{D}=[-\pi;\pi]\setminus\left\lbrace \displaystyle\frac{\pi}{4};\displaystyle\frac{3\pi}{4} \right\rbrace\).
Bài tập 14
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{\sqrt{4\pi^2-x^2}}{\cos 2x+1}\).
Điều kiện: \(\begin{cases} 4\pi^2-x^2\geq 0\\\cos 2x+1\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} 4\pi^2-x^2\geq 0\\\cos 2x\neq -1\end{cases}\) \(\Leftrightarrow \begin{cases}-2\pi\leq x\leq 2\pi\\2x\neq \pi+ k2\pi\end{cases}\) \(\Leftrightarrow \begin{cases}-2\pi\leq x\leq 2\pi\\x\neq \displaystyle\frac{\pi}{2}+k\pi.\end{cases}\)
Ta có \(-2\pi\leq \displaystyle\frac{\pi}{2}+k\pi\leq 2\pi\) \(\Leftrightarrow -\displaystyle\frac{5}{2}\leq k\leq \displaystyle\frac{3}{2}\).
Tập xác định \(\mathscr{D}=[-2\pi;2\pi]\setminus\left\lbrace \pm\displaystyle\frac{3\pi}{2};-\displaystyle\frac{\pi}{2};\displaystyle\frac{\pi}{2} \right\rbrace\).
Dạng 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Phương pháp giải
Bài tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=5-3 \cos 4 x \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&-1 \leq \cos 4 x \leq 1 \\\Leftrightarrow\ & 3 \geq-3 \cos 4 x \geq-3\\ \Leftrightarrow\ & 5+3 \geq 5-3 \cos 4 x \geq 5-3 \\ \Leftrightarrow\ & 2 \leq y \leq 8.\end{aligned}\)
\(\max y=8\) khi
\(\cos 4 x=-1 \Leftrightarrow x=\displaystyle\frac{\pi}{4}+\displaystyle\frac{k\pi}{2}\).
\(\min y=2\) khi
\(\cos 4 x=1 \Leftrightarrow x=\displaystyle\frac{k\pi}{2}\).
Bài tập 2
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=2+3 \cos x \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&-1 \leq \cos x \leq 1\\\Leftrightarrow\ & -3 \geq3 \cos x \geq-3\\ \Leftrightarrow\ &-1 \geq 2+3 \cos x \geq 5\\ \Leftrightarrow\ & -1 \leq y \leq 5. \end{aligned}\)
\(\max y=5 \) khi \( \cos x=1 \Leftrightarrow x=k2\pi\).
\( \min y=-1 \) khi \( \cos x=-1 \Leftrightarrow x=\pi +k2\pi\).
Bài tập 3
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=3-2 \sin 2 x \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&-1 \leq \sin 2x \leq 1\\ \Leftrightarrow\ & -2 \leq -2\sin 2x \leq 2\\ \Leftrightarrow\ & 1 \leq 3-2\sin 2x \leq 5\\ \Leftrightarrow\ & 1 \leq y \leq 5.\end{aligned}\)
\( \max y=5 \) khi \( \sin 2x=-1 \Leftrightarrow x=-\displaystyle\frac{\pi}{4}+k\pi\).
\( \min y=1 \) khi \( \sin 2x=1 \Leftrightarrow x=\displaystyle\frac{\pi}{4}+k\pi\).
Bài tập 4
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=3-2|\sin 2 x| \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&0\leq |\sin 2 x|\leq 1\\ \Leftrightarrow\ & -2\leq -2|\sin 2 x|\leq 0\\ \Leftrightarrow\ & 1\leq 3-2|\sin 2 x|\leq 3.\end{aligned}\)
\( \max y=3 \) khi \( \sin 2 x=0 \Leftrightarrow x=\displaystyle\frac{k\pi}{2}\).
\( \min y=1\) khi \( \sin 2 x=\pm1 \Leftrightarrow x=\displaystyle\frac{\pm\pi}{4}+k\pi\).
Bài tập 5
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=\displaystyle\frac{1+4 \cos ^{2} x}{3} \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}& 0\leq \cos ^{2} x \leq 1\\ \Leftrightarrow\ & 0\leq 4\cos ^{2} x \leq 4\\ \Leftrightarrow\ & 1\leq 1+4\cos ^{2} x \leq5\\ \Leftrightarrow\ & \displaystyle\frac{1}{3}\leq \displaystyle\frac{1+4\cos ^{2} x}{3} \leq \displaystyle\frac{5}{3}.\end{aligned}\)
\( \max y=\displaystyle\frac{5}{3} \) khi \( \cos x=0 \Leftrightarrow x=\displaystyle\frac{\pi}{2}+k\pi\).
\( \min y=\displaystyle\frac{1}{3} \) khi \( \cos x=\pm1 \Leftrightarrow x=k\pi\).
Bài tập 6
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=1-\displaystyle\frac{1}{2} \sin ^{2} 2 x \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}& 0 \leq \sin ^{2} 2 x \leq 1\\ \Leftrightarrow\ & -\displaystyle\frac{1}{2} \leq -\displaystyle\frac{1}{2}\cdot\sin ^{2} 2 x \leq 0\\ \Leftrightarrow\ & \displaystyle\frac{1}{2} \leq -\displaystyle\frac{1}{2}\cdot\sin ^{2} 2 x \leq 1.\end{aligned}\)
\( \max y=1 \) khi \( \sin 2 x=0 \Leftrightarrow x=\displaystyle\frac{\pi}{4}+\displaystyle\frac{k\pi}{2}\).
\( \min y=\displaystyle\frac{1}{2} \) khi \( \sin 2 x=\pm1 \Leftrightarrow x=\displaystyle\frac{\pi}{4}+\displaystyle\frac{k\pi}{2}\).
Bài tập 7
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=\sin x+\sin (x+2 \pi / 3) \).
Áp dụng công thức \fbox\( \sin a+\sin b=2 \sin \displaystyle\frac{a+b}{2} \cos \displaystyle\frac{a-b}{2} \), ta có
\(\begin{aligned}y=\ &\sin x + \sin \left (x+\displaystyle\frac{2\pi}{3}\right )\\ =\ &-\sin \left (x+\displaystyle\frac{\pi}{3}\right ).\end{aligned}\)
Tập xác định: \( \mathscr{D}=\mathbb{R}\).
\(\forall x \in \mathbb{R} \), ta có
\(\begin{aligned}-1 \leq -\sin \left (x+\displaystyle\frac{\pi}{3}\right ) \leq 1.\end{aligned}\)
\( \max y=1 \) khi \( \sin \left (x+\displaystyle\frac{\pi}{3}\right )=1 \Leftrightarrow x=\displaystyle\frac{\pi}{6}+k2\pi\).
\( \min y=-1 \) khi \( \sin \left (x+\displaystyle\frac{\pi}{3}\right )=-1 \Leftrightarrow x=-\displaystyle\frac{5\pi}{6}+k2\pi\).
Bài tập 8
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=\cos x+\cos (x+\pi / 3) \).
Áp dụng công thức \( \cos a+\cos b=2 \cos \displaystyle\frac{a+b}{2} \cos \displaystyle\frac{a-b}{2} \), ta có
\(\begin{aligned}y=\cos x+\cos \left (x+\displaystyle\frac{\pi}{3}\right )=\sqrt{3}\cos \left (x+\displaystyle\frac{\pi}{6}\right ).\end{aligned}\)
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&-1 \leq \cos \left (x+\displaystyle\frac{\pi}{6}\right ) \leq 1\\ \Leftrightarrow\ & -\sqrt{3} \leq \sqrt{3}\cos \left (x+\displaystyle\frac{\pi}{6}\right ) \leq \sqrt{3}.\end{aligned}\)
\( \max y=\sqrt{3} \) khi \( \cos \left (x+\displaystyle\frac{\pi}{6}\right ) =1 \Leftrightarrow x=-\displaystyle\frac{\pi}{6}+k2\pi\).
\( \min y=-\sqrt{3} \) khi \( \cos \left (x+\displaystyle\frac{\pi}{6}\right )=-1 \Leftrightarrow x=\displaystyle\frac{5\pi}{6}+k2\pi\).
Bài tập 9
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\displaystyle\frac{4}{2-\sin x}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \sin x\leq 1\\ \Leftrightarrow\ & -1\leq -\sin x\leq 1\\ \Leftrightarrow\ &1\leq 2-\sin x\leq 3\\ \Leftrightarrow\ & \displaystyle\frac{1}{3}\leq \displaystyle\frac{1}{2-\sin x}\leq 1\\ \Leftrightarrow\ & \displaystyle\frac{4}{3}\leq \displaystyle\frac{4}{2-\sin x}\leq 4.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=4\) khi \(x=\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=\displaystyle\frac{4}{3}\) khi \(x=-\displaystyle\frac{\pi}{2}\).
Bài tập 10
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\displaystyle\frac{8}{3-\cos ^{2} x}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& 0\leq \cos^2 x\leq 1\\ \Leftrightarrow\ & -1\leq -\cos^2 x\leq 0\\ \Leftrightarrow\ &2\leq 3-\cos^2 x\leq 3\\ \Leftrightarrow\ & \displaystyle\frac{8}{3}\leq \displaystyle\frac{8}{3-\cos^2 x}\leq 4.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=4\) khi \(x=0\) và \(\min\limits_{x \in \mathbb{R}} y=\displaystyle\frac{8}{3}\) khi \(x=\displaystyle\frac{\pi}{2}\).
Bài tập 11
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\displaystyle\frac{3}{3-\sqrt{1-\cos x}}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}&-1\leq \cos x\leq 1\\ \Leftrightarrow\ &-1\leq -\cos x\leq 1\\ \Leftrightarrow\ &0\leq \sqrt{1-\cos x}\leq \sqrt{2}\\ \Leftrightarrow\ &-\sqrt{2}\leq -\sqrt{1-\cos x}\leq 0\\ \Leftrightarrow\ &3-\sqrt{2}\leq 3 -\sqrt{1-\cos x}\leq 3\\ \Leftrightarrow\ &1\leq \displaystyle\frac{3}{3-\sqrt{1-\cos x}}\leq \displaystyle\frac{3}{3-\sqrt{2}}=\displaystyle\frac{9+3\sqrt{2}}{7}.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=\displaystyle\frac{9+3\sqrt{2}}{7}\) khi \(x=0\) và \(\min\limits_{x \in \mathbb{R}} y=1\) khi \(x=\pi\).
Bài tập 12
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\displaystyle\frac{1}{\sqrt{2-\sin ^{2} 3 x}}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& 0\leq \sin^2 3x\leq 1\\ \Leftrightarrow\ & -1\leq -\sin^2 3x\leq 0\\ \Leftrightarrow\ &1\leq 2-\sin^2 3x\leq 2\\ \Leftrightarrow\ &1\leq \sqrt{2-\sin^2 3x}\leq \sqrt{2}\\ \Leftrightarrow\ &\displaystyle\frac{1}{\sqrt{2}}\leq \displaystyle\frac{1}{\sqrt{2-\sin^2 3x}}\leq 1.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=1\) khi \(x=\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=\displaystyle\frac{\sqrt{2}}{2}\) khi \(x=0\).
Bài tập 13
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin x+\sqrt{3} \cos x+12\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi
\(\begin{aligned}y=\ &\sin x+\sqrt{3} \cos x+12\\ =\ &2\left(\displaystyle\frac{1}{2}\cdot\sin x+\displaystyle\frac{\sqrt{3}}{2}\cdot\cos x\right)+12\\ =\ &2\sin\left(x+\displaystyle\frac{\pi}{3}\right)+12.\end{aligned}\)
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}&-1\leq \sin\left(x+\displaystyle\frac{\pi}{3}\right)\leq 1\\ \Leftrightarrow\ & -2\leq 2\sin\left(x+\displaystyle\frac{\pi}{3}\right)\leq 2\\ \Leftrightarrow\ &10\leq 2\sin\left(x+\displaystyle\frac{\pi}{3}\right)+12\leq 14.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=14\) khi \(x=\displaystyle\frac{\pi}{6}\) và \(\min\limits_{x \in \mathbb{R}} y=10\) khi \(x=-\displaystyle\frac{5\pi}{6}\).
Bài tập 14
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{3} \sin x-\cos x+5\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi \(y=\sqrt{3} \sin x-\cos x+5=2\left(\displaystyle\frac{\sqrt{3}}{2}\cdot\sin x-\displaystyle\frac{1}{2}\cdot\cos x\right)+5=2\sin\left(x-\displaystyle\frac{\pi}{6}\right)+5\).\\
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \sin\left(x-\displaystyle\frac{\pi}{6}\right)\leq 1\\ \Leftrightarrow\ & -2\leq 2\sin\left(x-\displaystyle\frac{\pi}{6}\right)\leq 2\\ \Leftrightarrow\ &3\leq 2\sin\left(x-\displaystyle\frac{\pi}{6}\right)+5\leq 7.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=7\) khi \(x=\displaystyle\frac{2\pi}{3}\) và \(\min\limits_{x \in \mathbb{R}} y=3\) khi \(x=-\displaystyle\frac{\pi}{3}\).
Bài tập 15
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos 3x-\sqrt{3} \sin 3x+4\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi
\(\begin{aligned}y=\ &\cos 3x-\sqrt{3} \sin 3x+4\\ =\ &2\left(\displaystyle\frac{1}{2}\cdot\cos 3x -\displaystyle\frac{\sqrt{3}}{2}\cdot\sin 3x\right)+4\\ =\ &2\cos\left(3x+\displaystyle\frac{\pi}{3}\right)+4\end{aligned}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \cos\left(3x+\displaystyle\frac{\pi}{3}\right)\leq 1\\ \Leftrightarrow\ & -2\leq 2\cos\left(3x+\displaystyle\frac{\pi}{3}\right)\leq 2\\ \Leftrightarrow\ &2\leq 2\cos\left(3x+\displaystyle\frac{\pi}{3}\right)+4\leq 6.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=6\) khi \(x=-\displaystyle\frac{\pi}{9}\) và \(\min\limits_{x \in \mathbb{R}} y=2\) khi \(x=-\displaystyle\frac{4\pi}{9}\).
Bài tập 16
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{3}\left(\cos ^{4} x-\sin ^{4} x\right)+\sin 2 x+1\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi
\(\begin{aligned}y=& \sqrt{3}\left(\cos ^{2} x+\sin ^{2} x\right)\left(\cos ^{2} x-\sin ^{2} x\right)+\sin 2 x+1\\ =\ & \sqrt{3}\cos 2x+\sin 2 x+1\\ =\ & 2\left(\displaystyle\frac{\sqrt{3}}{2}\cdot\cos 2x +\displaystyle\frac{1}{2}\cdot\sin 2x\right)+1\\ =\ & 2\cos\left(2x-\displaystyle\frac{\pi}{6}\right)+1.\end{aligned}\)
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \cos\left(2x-\displaystyle\frac{\pi}{6}\right)\leq 1\\ \Leftrightarrow\ & -2\leq 2\cos\left(2x-\displaystyle\frac{\pi}{6}\right)\leq 2\\ \Leftrightarrow\ &-1\leq 2\cos\left(2x-\displaystyle\frac{\pi}{6}\right)+1\leq 3.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=3\) khi \(x=\displaystyle\frac{\pi}{12}\) và \(\min\limits_{x \in \mathbb{R}} y=-1\) khi \(x=\displaystyle\frac{7\pi}{12}\).
Bài tập 17
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=4 \sin ^{2} x-4 \sin x+3\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi \(y=4 \sin ^{2} x-4 \sin x+3=\left(2\sin x+1\right)^2+2\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \sin x\leq 1\\ \Leftrightarrow\ & -1\leq 2\sin x+1\leq 3\\ \Leftrightarrow\ &0\leq \left( 2\sin x+1\right)^2\leq 9\\ \Leftrightarrow\ &2\leq \left( 2\sin x+1\right)^2+2\leq 11.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=11\) khi \(x=\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=2\) khi \(\sin x=-\displaystyle\frac{1}{2}\).
Bài tập 18
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos ^{2} x-2 \cos x-4\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi \(y=\cos ^{2} x-2 \cos x-4=\left(\cos x-1\right)^2-5\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \cos x\leq 1\\ \Leftrightarrow\ & -2\leq \cos x-1\leq 0\\ \Leftrightarrow\ &0\leq \left( \cos x-1\right)^2\leq 4\\ \Leftrightarrow\ &-5\leq \left( \cos x-1\right)^2-5\leq -1.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=-1\) khi \(x=\pi\) và \(\min\limits_{x \in \mathbb{R}} y=-5\) khi \(x=0\).
Bài tập 19
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos ^{2} x+2 \sin x+2\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi \(y=\cos ^{2} x+2 \sin x+2=-\sin^2 x+2\sin x+3=-\left(\sin x-1\right)^2+4 \).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \sin x\leq 1\\ \Leftrightarrow\ & -2\leq \sin x-1\leq 0\\ \Leftrightarrow\ &0\leq \left( \sin x-1\right)^2\leq 4\\ \Leftrightarrow\ &-4\leq -\left( \sin x-1\right)^2\leq 0\\ \Leftrightarrow\ &0\leq -\left( \sin x-1\right)^2+4\leq 4.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=4\) khi \(x=\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=0\) khi \(x=-\displaystyle\frac{\pi}{2}\).
Bài tập 20
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos ^{4} x-2 \sin ^{2} x+1\) .
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi
\(\begin{aligned}y=\ &\cos ^{4} x-2 \sin ^{2} x+1\\ =\ &\cos ^{4} x-2 \left(1-\cos^2 x\right)+1\\ =\ &\cos ^{4} x+2 \cos ^{2} x-1\\ =\ &\left(\cos^2 x+1\right)^2-2\end{aligned}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& 0\leq \cos^2 x\leq 1\\ \Leftrightarrow\ & 1\leq \cos^2 x+1\leq 2\\ \Leftrightarrow\ &1\leq \left( \cos^2 x+1\right)^2\leq 4\\ \Leftrightarrow\ &-1\leq \left( \cos^2 x+1\right)^2-2\leq 2.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=2\) khi \(x=0\) và \(\min\limits_{x \in \mathbb{R}} y=-1\) khi \(x=\displaystyle\frac{\pi}{2}\).
Bài tập 21
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{5-4 \sin x+\sin ^{2} x}\).
Xét hàm số \(g(x)=5-4 \sin x+\sin ^{2} x\) trên \(\mathbb{R}\).
Ta có
\(g(x)=5-4 \sin x+\sin ^{2} x\) \(=\left(\sin x -2\right)^2+1\)
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& & -1\leq \sin x\leq 1\\ \Leftrightarrow\ &-3\leq \sin x-2\leq -1\\ \Leftrightarrow\ &1\leq \left( \sin x-2\right)^2\leq 9\\ \Leftrightarrow\ &2\leq \left( \sin x-2\right)^2+1\leq 10.\end{aligned}\)
Suy ra:
\(2\leq g(x)\leq 10 \Rightarrow \sqrt{2}\leq y\leq \sqrt{10}\).
Vậy \(\max\limits_{x \in \mathbb{R}} y=\sqrt{10}\) khi \(x=-\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=\sqrt{2}\) khi \(x=\displaystyle\frac{\pi}{2}\).
Bài tập 22
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{\cos ^{2} x+6 \cos x+14}\) .
Xét hàm số \(g(x)=\cos ^{2} x+6 \cos x+14\) trên \(\mathbb{R}\).
Ta có
\(g(x)=\cos ^{2} x+6 \cos x+14\) \(=\left(\cos x +3\right)^2+5\)
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \cos x\leq 1\\ \Leftrightarrow\ &2\leq \cos x+3\leq 4\\ \Leftrightarrow\ &4\leq \left( \cos x+3\right)^2\leq 16\\ \Leftrightarrow\ &9\leq \left( \cos x+3\right)^2+5\leq 21.\end{aligned}\)
Suy ra:
\(9\leq g(x)\leq 21 \Rightarrow 3\leq y\leq \sqrt{21}\).
Vậy \(\max\limits_{x \in \mathbb{R}} y=\sqrt{21}\) khi \(x=0\) và \(\min\limits_{x \in \mathbb{R}} y=3\) khi \(x=\pi\).
Bài tập 23
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=2(\sin x+\cos x)+\sin 2 x+3\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Đặt
\(t=\sin x+ \cos x=\sqrt{2}\sin \left(x+\displaystyle\frac{\pi}{4}\right)\), \(t\in \left[-\sqrt{2};\sqrt{2}\right]\).
Ta có
\(t^2=\left(\sin x+ \cos x\right)^2\) \(=1+2\sin x\cos x=1+\sin 2x\) \(\Rightarrow \sin 2x =t^2-1\).
Hàm số trở thành \(y=g(t)=t^2+2t+2\).
Bảng biến thiên của hàm số \(y=g(t)\) trên đoạn \( \left[-\sqrt{2};\sqrt{2}\right]\)

Vậy \(\max\limits_{x \in \mathbb{R}} y=4+2\sqrt{2}\) và \(\min\limits_{x \in \mathbb{R}} y=1\).
Bài tập 24
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin x+\cos x+2 \sin x \cos x-1\) .
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Đặt \(t=\sin x+ \cos x=\sqrt{2}\sin \left(x+\displaystyle\frac{\pi}{4}\right)\), \(t\in \left[-\sqrt{2};\sqrt{2}\right]\).
Ta có
\(t^2=\left(\sin x+ \cos x\right)^2=1+2\sin x\cos x\) \(\Rightarrow 2\sin x\cos x =t^2-1\).
Hàm số trở thành \(y=g(t)=t^2+t-2\). \\
Bảng biến thiên của hàm số \(y=g(t)\) trên đoạn \( \left[-\sqrt{2};\sqrt{2}\right]\)
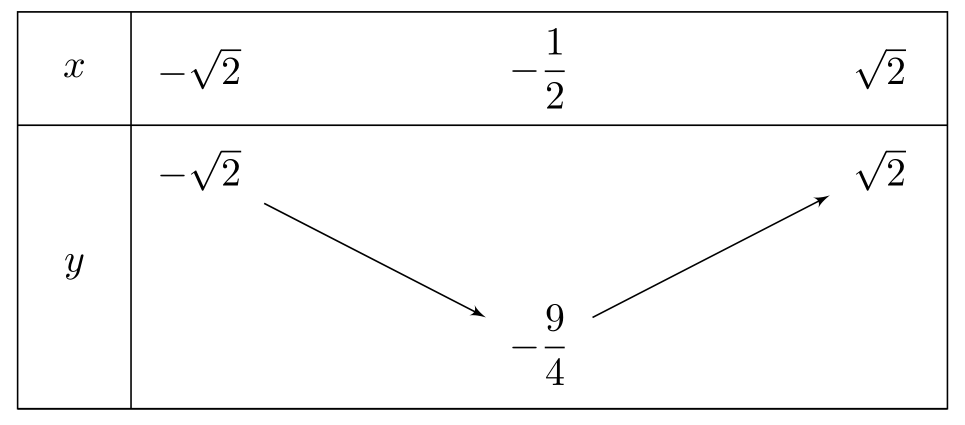
Vậy \(\max\limits_{x \in \mathbb{R}} y=\sqrt{2}\) và \(\min\limits_{x \in \mathbb{R}} y=-\displaystyle\frac{9}{4}\).
Bài tập 25
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=3-\sin 2 x\) trên đoạn \(\left[ 0; \displaystyle\frac{\pi}{2}\right]\)?
Ta có
\(x\in \left[ 0; \displaystyle\frac{\pi}{2}\right]\Rightarrow 2x\in \left[ 0; \pi\right]\).

Với mọi \(2x\in \left[ 0; \pi\right]\) ta có
\(\begin{aligned}& 0\leq \sin 2x\leq 1\\ \Leftrightarrow\ & -1\leq -\sin 2x\leq 0\\ \Leftrightarrow\ &2\leq 3-\sin 2x\leq 3.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[ 0; \tfrac{\pi}{2}\right]} y=3\) khi \(x=0\) và \(\min\limits_{x \in \left[ 0; \tfrac{\pi}{2}\right]} y=2\) khi \(x=\displaystyle\frac{\pi}{4}\).
Bài tập 26
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin 2 x+2\) trên \(\left[ 0; \displaystyle\frac{\pi}{2}\right]\)?
Ta có \(x\in \left[ 0; \displaystyle\frac{\pi}{2}\right]\Rightarrow 2x\in \left[ 0; \pi\right]\).

Với mọi \(2x\in \left[ 0; \pi\right]\) ta có
\(\begin{aligned}& 0\leq \sin 2x\leq 1\\ \Leftrightarrow\ &2\leq \sin 2x+2\leq 3.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[ 0; \tfrac{\pi}{2}\right]} y=3\) khi \(x=\displaystyle\frac{\pi}{4}\) và \(\min\limits_{x \in \left[ 0; \tfrac{\pi}{2}\right]} y=2\) khi \(x=0\).
Bài tập 27
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos \left(x+\displaystyle\frac{\pi}{3}\right)\) trên \([0 ; \pi]\).
Ta có
\(x\in \left[ 0; \pi\right]\) \(\Rightarrow x+\displaystyle\frac{\pi}{3}\in \left[ \displaystyle\frac{\pi}{3}; \displaystyle\frac{4\pi}{3}\right]\).

Do đó: \( -1 \leq \cos \left(x+\displaystyle\frac{\pi}{3}\right)\leq \displaystyle\frac{1}{2}\).
Vậy \(\max\limits_{x \in [0 ; \pi]} y=\displaystyle\frac{1}{2}\) khi \(x=0\) và \(\min\limits_{x \in [0 ; \pi]} y=-1\) khi \(x=\displaystyle\frac{2\pi}{3}\).
Bài tập 28
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin \left(2 x+\displaystyle\frac{\pi}{4}\right)+\displaystyle\frac{1}{2}\) trên \(\left[-\displaystyle\frac{\pi}{4} ; \displaystyle\frac{\pi}{4}\right]\).
Ta có \(x\in \left[ -\displaystyle\frac{\pi}{4}; \displaystyle\frac{\pi}{4}\right]\) \(\Rightarrow 2x+\displaystyle\frac{\pi}{4}\in \left[-\displaystyle\frac{\pi}{4}; \displaystyle\frac{3\pi}{4}\right]\).

Do đó:
\(\begin{aligned}& -\displaystyle\frac{\sqrt{2}}{2}\leq \sin \left(2 x+\displaystyle\frac{\pi}{4}\right)\leq 1\\ \Rightarrow\ & \displaystyle\frac{1-\sqrt{2}}{2}\leq \sin \left(2 x+\displaystyle\frac{\pi}{4}\right)+\displaystyle\frac{1}{2}\leq \displaystyle\frac{3}{2}.\end{aligned}\)
Vậy \(\max\limits_{x \in\left[-\tfrac{\pi}{4} ; \tfrac{\pi}{4}\right]} y=\displaystyle\frac{3}{2}\) và \(\min\limits_{x \in \left[-\tfrac{\pi}{4} ; \tfrac{\pi}{4}\right]} y=\displaystyle\frac{1-\sqrt{2}}{2}\).
Bài tập 29
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin^4 x+\cos^4 x-1\) = trên \(\left[0 ; \displaystyle\frac{\pi}{6}\right]\).
Ta có
\(\begin{aligned}&\sin^4 x+\cos^4 x\\ =\ & \left(\sin^2 x+\cos^2 x\right)^2-2\sin^2 x\cdot \cos^2 x\\ =\ &1-\displaystyle\frac{1}{2}\sin^2 2x\\ =\ &1-\displaystyle\frac{1-\cos 4x}{4}\\ =\ &\displaystyle\frac{3}{4}+\displaystyle\frac{1}{4}\cos 4x.\end{aligned}\)
Suy ra:
\(y=\sin^4 x+\cos^4 x-1=\displaystyle\frac{1}{4}\cos 4x-\displaystyle\frac{1}{4}\).

Do \(x\in \left[ 0 ; \displaystyle\frac{\pi}{6}\right]\Rightarrow 4x \in \left[0; \displaystyle\frac{2\pi}{3}\right]\).
Do đó:
\(\begin{aligned}& -\displaystyle\frac{1}{2}\leq\cos 4x \leq 1\\ \Leftrightarrow\ & -\displaystyle\frac{1}{8}\leq \displaystyle\frac{1}{4}\cos 4x \leq \displaystyle\frac{1}{4}\\ \Leftrightarrow\ & -\displaystyle\frac{3}{8}\leq \displaystyle\frac{1}{4}\cos 4x-\displaystyle\frac{1}{4} \leq 0.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[0 ; \tfrac{\pi}{6}\right]} y=0\) và \(\min\limits_{x \in \left[0 ; \tfrac{\pi}{6}\right]} y=-\displaystyle\frac{3}{8}\).
Bài tập 30
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin^6 x+\cos^6 x\) trên \(\left[-\displaystyle\frac{\pi}{2} ; \displaystyle\frac{\pi}{2}\right]\).
Ta có
\(\begin{aligned}&\sin^6 x+\cos^6 x\\ =\ & \left(\sin^2 x+\cos^2 x\right)^3-3\sin^2 x\cdot \cos^2 x\left(\sin^2 x+\cos^2 x \right)\\ =\ &1-\displaystyle\frac{3}{4}\sin^2 2x\\ =\ &1-\displaystyle\frac{3}{4}\cdot \displaystyle\frac{1-\cos 4x}{2}\\ =\ &\displaystyle\frac{5}{8}+\displaystyle\frac{3}{8}\cos 4x.\end{aligned}\)
Suy ra:
\(y=\sin^6 x+\cos^6 x = \displaystyle\frac{5}{8}+\displaystyle\frac{3}{8}\cos 4x\).
Do \(x\in \left[-\displaystyle\frac{\pi}{2} ; \displaystyle\frac{\pi}{2} \right]\Rightarrow 4x \in \left[-2\pi ; 2\pi\right]\) nên
\(\begin{aligned}& -1\leq\cos 4x \leq 1\\ \Leftrightarrow\ & -\displaystyle\frac{3}{8}\leq \displaystyle\frac{3}{8}\cos 4x \leq \displaystyle\frac{3}{8}\\ \Leftrightarrow\ & \displaystyle\frac{1}{4}\leq \displaystyle\frac{5}{8}+ \displaystyle\frac{3}{8}\cos 4x \leq 1.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[-\tfrac{\pi}{2} ; \tfrac{\pi}{2}\right]} y=1\) và \(\min\limits_{x \in \left[-\tfrac{\pi}{2} ; \tfrac{\pi}{2}\right]} y=\displaystyle\frac{1}{4}\).
Bài tập 31
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{3} \sin 2 x+2 \cos^2 x+3\) trên \(\left[-\displaystyle\frac{5 \pi}{6}; \displaystyle\frac{\pi}{4}\right]\).
Ta có
\(\begin{aligned}y=\ & \sqrt{3} \sin 2 x+2 \cos^2 x+3\\ =\ &\sqrt{3} \sin 2 x+2\cdot\displaystyle\frac{1+\cos 2x}{2}+3\\ =\ & \sqrt{3} \sin 2 x+\cos 2x+4\\ =\ &2\sin \left(2x+\displaystyle\frac{\pi}{6}\right)+4.\end{aligned}\)
Do \(x\in \left[-\displaystyle\frac{5 \pi}{6}; \displaystyle\frac{\pi}{4}\right]\) \(\Rightarrow 2x \in \left[-\displaystyle\frac{5 \pi}{3}; \displaystyle\frac{\pi}{2}\right]\) \(\Rightarrow 2x +\displaystyle\frac{\pi}{6}\in \left[-\displaystyle\frac{3\pi}{2}; \displaystyle\frac{2\pi}{3}\right]\) .
Do đó:
\(\begin{aligned}& -1\leq \sin \left(2x+\displaystyle\frac{\pi}{6}\right) \leq 1\\ \Leftrightarrow\ & -2\leq 2\sin \left(2x+\displaystyle\frac{\pi}{6}\right) \leq 2\\ \Leftrightarrow\ & 2\leq 2\sin \left(2x+\displaystyle\frac{\pi}{6}\right)+4 \leq 6.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[-\tfrac{5 \pi}{6}; \tfrac{\pi}{4}\right]} y=6\) và \(\min\limits_{x \in \left[-\tfrac{5 \pi}{6}; \tfrac{\pi}{4}\right]} y=2\).
Bài tập 32
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin 2 x+\cos 2 x+3\) trên \(\left[-\displaystyle\frac{\pi}{4} ; \displaystyle\frac{\pi}{4}\right]\).
Ta có \(y= \sin 2 x+\cos 2 x+3= \sqrt{2}\sin \left(2x+\displaystyle\frac{\pi}{4}\right)+3\).
Do \(x\in \left[-\displaystyle\frac{\pi}{4} ; \displaystyle\frac{\pi}{4}\right]\Rightarrow 2x \in \left[-\displaystyle\frac{\pi}{2} ; \displaystyle\frac{\pi}{2}\right]\) \(\Rightarrow 2x +\displaystyle\frac{\pi}{4}\in \left[-\displaystyle\frac{\pi}{4}; \displaystyle\frac{3\pi}{4}\right]\).

Do đó:
\(\begin{aligned}& -\displaystyle\frac{\sqrt{2}}{2}\leq\sin \left(2x+\displaystyle\frac{\pi}{4}\right) \leq 1\\ \Leftrightarrow\ & -1\leq \sqrt{2} \sin \left(2x+\displaystyle\frac{\pi}{4}\right)\leq \sqrt{2}\\ \Leftrightarrow\ & 2\leq \sqrt{2}\sin \left(2x+\displaystyle\frac{\pi}{4}\right)+3 \leq 3+\sqrt{2}.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[-\tfrac{\pi}{4} ; \tfrac{\pi}{4}\right]} y=3+\sqrt{2}\) và \(\min\limits_{x \in \left[-\tfrac{\pi}{4} ; \tfrac{\pi}{4}\right]} y=2\).
Dạng 3. Xét tính chẵn lẻ của hàm số lượng giác
Phương pháp giải
Bài tập 1
Xét tính chẵn, lẻ của hàm số \(f(x)=\sin^2 2x+\cos 3x\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\sin^2(-2x)+\cos(-3x)\) \(=\sin^2 2x+\cos 3x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 2
Xét tính chẵn, lẻ của hàm số \(f(x)=\cos^2 3x+\cos x\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\cos^2(-3x)+\cos(-x)\) \(=\cos^2 3x+\cos x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 3
Xét tính chẵn, lẻ của hàm số \(f(x)=\displaystyle\frac{\sin^2 x-\cos x}{\sin 3x}\).
Điều kiện xác định \(\sin 3x\ne0\Leftrightarrow x\ne\displaystyle\frac{k\pi}{3}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{3},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\displaystyle\frac{\sin^2(-x)-\cos(-x)}{\sin(-3x)}\) \(=\displaystyle\frac{\sin^2 x-\cos x}{-\sin 3x}=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Bài tập 4
Xét tính chẵn, lẻ của hàm số \(f(x)=1+\cos x\cdot\sin\left(\displaystyle\frac{3\pi}{2}-2x\right)\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(x)=1+\cos x\cdot\sin\left(\displaystyle\frac{3\pi}{2}-2x\right)\) \(=1-\cos x\cdot\sin\left(\displaystyle\frac{\pi}{2}-2x\right)\) \(=1-\cos x\cdot\cos 2x\).
Khi đó
\(f(-x)=1-\cos(-x)\cdot\cos(-2x)\) \(=1-\cos x\cdot\cos 2x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 5
Xét tính chẵn, lẻ của hàm số \(f(x)=\cos\sqrt{x^2-16}\).
Điều kiện xác định của hàm số là \(x^2-16\ge0\Leftrightarrow\left[\begin{aligned}x\ge4\\ x\le-4.\end{aligned}\right.\)
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus(-4;4)\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\cos\sqrt{(-x)^2-16}\) \(=\cos\sqrt{x^2-16}=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 6
Xét tính chẵn, lẻ của hàm số \(f(x)=\tan x+\cot x\).
Điều kiện xác định của hàm số là \(\begin{cases}\sin x\ne0\\ \cos x\ne0\end{cases}\Leftrightarrow x\ne\displaystyle\frac{k\pi}{2}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{2},\ k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\tan(-x)+\cot(-x)\) \(=-\tan x-\cot x=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Bài tập 7
Xét tính chẵn, lẻ của hàm số \(f(x)=\cot(4x+5\pi)\cdot\tan(2x-3\pi)\).
Ta có
\(f(x)=\cot(4x+5\pi)\cdot\tan(2x-3\pi)\) \(=\cot 4x\cdot\tan 2x\).
Điều kiện xác định của hàm số là
\(\begin{cases}\sin 4x\ne0\\ \cos 2x\ne0\end{cases}\) \(\Leftrightarrow\begin{cases}x\ne\displaystyle\frac{k\pi}{4}\\ x\ne\displaystyle\frac{\pi}{4}+\displaystyle\frac{k\pi}{2}\end{cases}\) \(\Leftrightarrow x\ne\displaystyle\frac{k\pi}{4}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{4},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\cot(-4x)\cdot\tan(-2x)\) \(=\cot 4x\cdot\tan 2x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 8
Xét tính chẵn, lẻ của hàm số \(f(x)=\sin^3(3x+\pi)+\cot(2x-7\pi)\).
Ta có
\(f(x)=\sin^3(3x+\pi)+\cot(2x-7\pi)\) \(=-\sin^3 x+\cot 2x\).
Điều kiện xác định của hàm số là \(\sin 2x\ne0\Leftrightarrow x\ne\displaystyle\frac{k\pi}{2}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{2},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=-\sin^3(-x)+\cot(-2x)\) \(=\sin^3 x-\cot 2x=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Bài tập 9
Xét tính chẵn, lẻ của hàm số \(f(x)=\left|\sin x-\displaystyle\frac{1}{2}\right|+\left|\sin x+\displaystyle\frac{1}{2}\right|\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng. Ta có
\(\begin{aligned}f(-x)=\ &\left|\sin (-x)-\displaystyle\frac{1}{2}\right|+\left|\sin (-x)+\displaystyle\frac{1}{2}\right|\\ =\ &\left|-\sin x-\displaystyle\frac{1}{2}\right|+\left|-\sin x+\displaystyle\frac{1}{2}\right|\\ =\ &\left|\sin x+\displaystyle\frac{1}{2}\right|+\left|\sin x-\displaystyle\frac{1}{2}\right|\\ =\ &f(x),\,\forall x\in\mathscr{D}.\end{aligned}\)
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 10
Xét tính chẵn, lẻ của hàm số \(f(x)=\displaystyle\frac{\sqrt{\cos x+2}+\cot^2 x}{\sin 4x}\).
Điều kiện xác định
\(\begin{cases}\cos x+2\ge 0\\ \sin x\ne 0\\ \sin 4x\ne 0\end{cases}\) \(\Leftrightarrow\begin{cases}\cos x\ge -2\\ \sin 4x\ne 0\end{cases}\) \(\Leftrightarrow 4x\ne k\pi\) \(\Leftrightarrow x\ne\displaystyle\frac{k\pi}{4}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{4},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\displaystyle\frac{\sqrt{\cos(-x)+2}+\cot^2(-x)}{\sin(-4x)}\) \(=\displaystyle\frac{\sqrt{\cos x+2}+\cot^2 x}{-\sin 4x}=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Dạng 4. Tìm chu kì của hàm số lượng giác
Phương pháp giải
Bài tập 1
Hàm số \(y=\sin 2x\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=2\pi\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=\pi\)
D. \(T_0=4\pi\)
Ta có hàm số \(y=\sin 2x\) tuần hoàn với chu kỳ \(T_0=\displaystyle\frac{2\pi}{2}=\pi\).
Bài tập 2
Hàm số \(y=\tan 2x\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=\displaystyle\frac{\pi}{3}\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=2\pi\)
D. \(T_0=\pi\)
Ta có hàm số \(y=\tan 2x\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{\pi}{2}\).
Bài tập 3
Hàm số \(y=3\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=0\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=2\pi\)
D. \(T_0=4\pi\)
Ta có hàm số \(y=3\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{2\pi}{\tfrac{1}{2}}=4\pi\).
Bài tập 4
Hàm số \(f(x)=\sin\displaystyle\frac{x}{2}+2\cos\displaystyle\frac{3x}{2}\) tuần hoàn với chu kỳ chu kỳ là
A. \(5\pi\)
B. \(\displaystyle\frac{\pi}{2}\)
C. \(3\pi\)
D. \(4\pi\)
Ta có
+) hàm số \(\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ \(T_1=\displaystyle\frac{2\pi}{\tfrac{1}{2}}=4\pi\),
+) hàm số \(\cos\displaystyle\frac{3x}{2}\) tuần hoàn với chu kỳ \(T_2=\displaystyle\frac{2\pi}{\tfrac{3}{2}}=\displaystyle\frac{4\pi}{3}\).
Do đó hàm số \(f(x)\) tuần hoàn với chu kỳ \(T_0\) là bội chung nhỏ nhất của \(T_1\) và \(T_2\).
Do \(T_1\) là bội của \(T_2\) \(\left(\displaystyle\frac{T_1}{T_2}=3\right)\) nên \(T_0=T_1\).
Vậy hàm số \(f(x)\) đã cho tuần hoàn với chu kỳ \(T_0=4\pi\).
Bài tập 5
Tìm \(m\) để hàm số \(y=\cos mx\) tuần hoàn với chu kỳ \(T_0=\pi\).
A. \(m=\pm1\)
B. \(m=\pm2\)
C. \(m=\pm\displaystyle\frac{\pi}{2}\)
D. \(m=\pm\pi\)
Ta có hàm số \(y=\cos mx\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{2\pi}{|m|}\).
Để hàm số tuần hoàn với chu kỳ \(T_0=\pi\) thì
\(T=T_0\Leftrightarrow \displaystyle\frac{2\pi}{|m|}=\pi\Leftrightarrow |m|=2\Leftrightarrow m=\pm2\).
Bài tập 1
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{\tan 2x}{\cos x+1}+\sin x\).
Điều kiện:
\(\begin{cases}\cos x+1\neq 0\\ \cos 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases}\cos x\neq -1\\ \cos 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq \pi +k2\pi\\2x\neq \displaystyle\frac{\pi}{2}+k\pi\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq \pi +k2\pi\\x\neq \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2}.\end{cases}\)
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace\pi +k2\pi;\, \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2},\, k\in \mathbb{Z} \right\rbrace\).
Bài tập 2
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{\cos 3x}{1-\sin x}+\tan x\).
Điều kiện:
\(\begin{cases}1-\sin x\neq 0\\ \cos x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases}\sin x\neq 1\\ \cos x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq \displaystyle\frac{\pi}{2} +k2\pi\\x\neq \displaystyle\frac{\pi}{2}+k\pi\end{cases}\) \(\Leftrightarrow x\neq \displaystyle\frac{\pi}{2}+k\pi\).
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace \displaystyle\frac{\pi}{2}+k\pi,\, k\in \mathbb{Z} \right\rbrace\).
Bài tập 3
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{2\tan 2x-5}{\sin 2x+1}\).
Điều kiện:
\(\begin{cases}\sin 2x+1\neq 0\\ \cos 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases}\sin 2x\neq -1\\ \cos 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} 2x\neq -\displaystyle\frac{\pi}{2} +k2\pi\\2x\neq \displaystyle\frac{\pi}{2}+k\pi\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq -\displaystyle\frac{\pi}{4} +k\pi\\x\neq \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2}\end{cases}\) \(\Leftrightarrow x\neq \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2}, \, k\in \mathbb{Z} \right\rbrace\).
Bài tập 4
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{1}{\tan x-1}\).
Điều kiện:
\(\begin{cases}\tan x-1\neq 0\\ \cos x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases}\tan x\neq 1\\ \cos x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq \displaystyle\frac{\pi}{4} +k\pi\\x\neq \displaystyle\frac{\pi}{2}+k\pi.\end{cases}\)
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace\displaystyle\frac{\pi}{4} +k\pi;\, \displaystyle\frac{\pi}{2}+k\pi,\, k\in \mathbb{Z} \right\rbrace\).
Bài tập 5
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{3}{\cos^2 x-\sin^2 x}+\tan x\).
Ta có \(y=\displaystyle\frac{3}{\cos^2 x-\sin^2 x}+\tan x=\displaystyle\frac{3}{\cos 2x}+\tan x\).
Điều kiện:
\(\begin{cases}\cos x\neq 0\\ \cos 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq \displaystyle\frac{\pi}{2} +k\pi\\2x\neq \displaystyle\frac{\pi}{2}+k\pi\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq \displaystyle\frac{\pi}{2} +k\pi\\x\neq \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2}.\end{cases}\)
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace\displaystyle\frac{\pi}{2} +k\pi;\, \displaystyle\frac{\pi}{4}+k\displaystyle\frac{\pi}{2},\, k\in \mathbb{Z} \right\rbrace\).
Bài tập 6
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{1}{\sin x}+\displaystyle\frac{1}{\cos x}\).
Điều kiện:
\(\begin{cases}\cos x\neq 0\\ \sin x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} x\neq k\pi\\x\neq \displaystyle\frac{\pi}{2}+k\pi\end{cases}\) \(\Leftrightarrow x\neq k\displaystyle\frac{\pi}{2}.\)
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace k\displaystyle\frac{\pi}{2},\, k\in \mathbb{Z} \right\rbrace\).
Bài tập 7
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\sqrt{\displaystyle\frac{2-\sin x}{\cos x+1}}\).
Điều kiện: \(\displaystyle\frac{2-\sin x}{\cos x+1}\geq 0\).
Với mọi \(x\in \mathbb{R}\), ta có
\(-1\leq \sin x\leq 1\Leftrightarrow 1\leq 2-\sin x\leq 3;\)
\(-1\leq \cos x\leq 1\Leftrightarrow 0\leq \cos x+1\leq 2.\)
Do đó
\(\displaystyle\frac{2-\sin x}{\cos x+1}\geq 0\Leftrightarrow \cos x+1\neq 0\) \(\Leftrightarrow \cos x\neq -1\Leftrightarrow x\neq \pi +k2\pi.\)
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace \pi +k2\pi, \, k\in \mathbb{Z} \right\rbrace\).
Bài tập 8
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{1}{\sqrt{1-\sin x}}\).
Điều kiện:
\(1-\sin x> 0\Leftrightarrow \sin x<1\) \(\Leftrightarrow \sin x \neq 1\Leftrightarrow x \neq \displaystyle\frac{\pi}{2}+k2\pi\).
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace \displaystyle\frac{\pi}{2}+k2\pi, \, k\in \mathbb{Z} \right\rbrace\).
Bài tập 9
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\sqrt{\displaystyle\frac{\cos x+4}{\sin x+1}}\).
Điều kiện: \(\displaystyle\frac{\cos x+4}{\sin x+1}\geq 0\).
Với mọi \(x\in \mathbb{R}\), ta có
\(-1\leq \sin x\leq 1\Leftrightarrow 0\leq \sin x+1\leq 2;\)
\(-1\leq \cos x\leq 1\Leftrightarrow 3\leq \cos x+4\leq 5.\)
Do đó
\(\displaystyle\frac{\cos x+4}{\sin x+1}\geq 0\Leftrightarrow \sin x+1\neq 0\) \(\Leftrightarrow \sin x\neq -1\Leftrightarrow x\neq -\displaystyle\frac{\pi}{2} +k2\pi\).
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace -\displaystyle\frac{\pi}{2} +k2\pi, \, k\in \mathbb{Z} \right\rbrace\).
Bài tập 10
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\sqrt{\displaystyle\frac{2-\cos x}{1-\sin x}}\).
Điều kiện: \(\displaystyle\frac{2-\cos x}{1-\sin x}\geq 0\).
Với mọi \(x\in \mathbb{R}\), ta có
\(-1\leq \sin x\leq 1\Leftrightarrow 0\leq 1-\sin x\leq 2;\)
\(-1\leq \cos x\leq 1\Leftrightarrow 1\leq 2-\cos x\leq 3.\)
Do đó
\(\displaystyle\frac{2-\cos x}{1-\sin x}\geq 0\Leftrightarrow 1-\sin x\neq 0 \Leftrightarrow \sin x\neq 1\Leftrightarrow x\neq \displaystyle\frac{\pi}{2} +k2\pi\).
Tập xác định \(\mathscr{D}=\mathbb{R}\setminus\left\lbrace \displaystyle\frac{\pi}{2} +k2\pi, \, k\in \mathbb{Z} \right\rbrace\).
Bài tập 11
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\sqrt{4\pi^2-x^2}+\cot 2x\).
Điều kiện:
\(\begin{cases} 4\pi^2-x^2\geq 0\\\sin 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases}-2\pi\leq x\leq 2\pi\\2x\neq k\pi\end{cases}\) \(\Leftrightarrow \begin{cases}-2\pi\leq x\leq 2\pi\\x\neq k\displaystyle\frac{\pi}{2}.\end{cases}\)
Ta có
\(-2\pi\leq k\displaystyle\frac{\pi}{2}\leq 2\pi\Leftrightarrow -4\leq k\leq 4\).
Tập xác định \(\mathscr{D}=(-2\pi;2\pi)\setminus\left\lbrace \pm \displaystyle\frac{3\pi}{2};\pm \pi; \pm\displaystyle\frac{\pi}{2};0 \right\rbrace\).
Bài tập 12
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\sqrt{\pi^2-x^2}+\cot 2x\).
Điều kiện:
\(\begin{cases} \pi^2-x^2\geq 0\\\sin 2x\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases}-\pi\leq x\leq \pi\\2x\neq k\pi\end{cases}\) \(\Leftrightarrow \begin{cases}-\pi\leq x\leq \pi\\x\neq k\displaystyle\frac{\pi}{2}.\end{cases}\)
Ta có \(-\pi\leq k\displaystyle\frac{\pi}{2}\leq \pi\Leftrightarrow -2\leq k\leq 2\).
Tập xác định \(\mathscr{D}=(-\pi;\pi)\setminus\left\lbrace\pm\displaystyle\frac{\pi}{2};0 \right\rbrace\).
Bài tập 13
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{\sqrt{\pi^2-x^2}}{\sin 2x+1}\).
Điều kiện: \(\begin{cases} \pi^2-x^2\geq 0\\\sin 2x+1\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} \pi^2-x^2\geq 0\\\sin 2x\neq -1\end{cases}\) \(\Leftrightarrow \begin{cases}-\pi\leq x\leq \pi\\2x\neq -\displaystyle\frac{\pi}{2}+ k2\pi\end{cases}\) \(\Leftrightarrow \begin{cases}-\pi\leq x\leq \pi\\x\neq -\displaystyle\frac{\pi}{4}+k\pi.\end{cases}\)
Ta có
\(-\pi\leq -\displaystyle\frac{\pi}{4}+k\pi\leq \pi\) \(\Leftrightarrow -\displaystyle\frac{3}{4}\leq k\leq \displaystyle\frac{5}{4}\).
Tập xác định \(\mathscr{D}=[-\pi;\pi]\setminus\left\lbrace \displaystyle\frac{\pi}{4};\displaystyle\frac{3\pi}{4} \right\rbrace\).
Bài tập 14
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\displaystyle\frac{\sqrt{4\pi^2-x^2}}{\cos 2x+1}\).
Điều kiện: \(\begin{cases} 4\pi^2-x^2\geq 0\\\cos 2x+1\neq 0\end{cases}\) \(\Leftrightarrow \begin{cases} 4\pi^2-x^2\geq 0\\\cos 2x\neq -1\end{cases}\) \(\Leftrightarrow \begin{cases}-2\pi\leq x\leq 2\pi\\2x\neq \pi+ k2\pi\end{cases}\) \(\Leftrightarrow \begin{cases}-2\pi\leq x\leq 2\pi\\x\neq \displaystyle\frac{\pi}{2}+k\pi.\end{cases}\)
Ta có \(-2\pi\leq \displaystyle\frac{\pi}{2}+k\pi\leq 2\pi\) \(\Leftrightarrow -\displaystyle\frac{5}{2}\leq k\leq \displaystyle\frac{3}{2}\).
Tập xác định \(\mathscr{D}=[-2\pi;2\pi]\setminus\left\lbrace \pm\displaystyle\frac{3\pi}{2};-\displaystyle\frac{\pi}{2};\displaystyle\frac{\pi}{2} \right\rbrace\).
Dạng 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Phương pháp giải
Bài tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=5-3 \cos 4 x \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&-1 \leq \cos 4 x \leq 1 \\\Leftrightarrow\ & 3 \geq-3 \cos 4 x \geq-3\\ \Leftrightarrow\ & 5+3 \geq 5-3 \cos 4 x \geq 5-3 \\ \Leftrightarrow\ & 2 \leq y \leq 8.\end{aligned}\)
\(\max y=8\) khi
\(\cos 4 x=-1 \Leftrightarrow x=\displaystyle\frac{\pi}{4}+\displaystyle\frac{k\pi}{2}\).
\(\min y=2\) khi
\(\cos 4 x=1 \Leftrightarrow x=\displaystyle\frac{k\pi}{2}\).
Bài tập 2
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=2+3 \cos x \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&-1 \leq \cos x \leq 1\\\Leftrightarrow\ & -3 \geq3 \cos x \geq-3\\ \Leftrightarrow\ &-1 \geq 2+3 \cos x \geq 5\\ \Leftrightarrow\ & -1 \leq y \leq 5. \end{aligned}\)
\(\max y=5 \) khi \( \cos x=1 \Leftrightarrow x=k2\pi\).
\( \min y=-1 \) khi \( \cos x=-1 \Leftrightarrow x=\pi +k2\pi\).
Bài tập 3
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=3-2 \sin 2 x \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&-1 \leq \sin 2x \leq 1\\ \Leftrightarrow\ & -2 \leq -2\sin 2x \leq 2\\ \Leftrightarrow\ & 1 \leq 3-2\sin 2x \leq 5\\ \Leftrightarrow\ & 1 \leq y \leq 5.\end{aligned}\)
\( \max y=5 \) khi \( \sin 2x=-1 \Leftrightarrow x=-\displaystyle\frac{\pi}{4}+k\pi\).
\( \min y=1 \) khi \( \sin 2x=1 \Leftrightarrow x=\displaystyle\frac{\pi}{4}+k\pi\).
Bài tập 4
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=3-2|\sin 2 x| \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&0\leq |\sin 2 x|\leq 1\\ \Leftrightarrow\ & -2\leq -2|\sin 2 x|\leq 0\\ \Leftrightarrow\ & 1\leq 3-2|\sin 2 x|\leq 3.\end{aligned}\)
\( \max y=3 \) khi \( \sin 2 x=0 \Leftrightarrow x=\displaystyle\frac{k\pi}{2}\).
\( \min y=1\) khi \( \sin 2 x=\pm1 \Leftrightarrow x=\displaystyle\frac{\pm\pi}{4}+k\pi\).
Bài tập 5
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=\displaystyle\frac{1+4 \cos ^{2} x}{3} \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}& 0\leq \cos ^{2} x \leq 1\\ \Leftrightarrow\ & 0\leq 4\cos ^{2} x \leq 4\\ \Leftrightarrow\ & 1\leq 1+4\cos ^{2} x \leq5\\ \Leftrightarrow\ & \displaystyle\frac{1}{3}\leq \displaystyle\frac{1+4\cos ^{2} x}{3} \leq \displaystyle\frac{5}{3}.\end{aligned}\)
\( \max y=\displaystyle\frac{5}{3} \) khi \( \cos x=0 \Leftrightarrow x=\displaystyle\frac{\pi}{2}+k\pi\).
\( \min y=\displaystyle\frac{1}{3} \) khi \( \cos x=\pm1 \Leftrightarrow x=k\pi\).
Bài tập 6
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=1-\displaystyle\frac{1}{2} \sin ^{2} 2 x \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}& 0 \leq \sin ^{2} 2 x \leq 1\\ \Leftrightarrow\ & -\displaystyle\frac{1}{2} \leq -\displaystyle\frac{1}{2}\cdot\sin ^{2} 2 x \leq 0\\ \Leftrightarrow\ & \displaystyle\frac{1}{2} \leq -\displaystyle\frac{1}{2}\cdot\sin ^{2} 2 x \leq 1.\end{aligned}\)
\( \max y=1 \) khi \( \sin 2 x=0 \Leftrightarrow x=\displaystyle\frac{\pi}{4}+\displaystyle\frac{k\pi}{2}\).
\( \min y=\displaystyle\frac{1}{2} \) khi \( \sin 2 x=\pm1 \Leftrightarrow x=\displaystyle\frac{\pi}{4}+\displaystyle\frac{k\pi}{2}\).
Bài tập 7
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=\sin x+\sin (x+2 \pi / 3) \).
Áp dụng công thức \fbox\( \sin a+\sin b=2 \sin \displaystyle\frac{a+b}{2} \cos \displaystyle\frac{a-b}{2} \), ta có
\(\begin{aligned}y=\ &\sin x + \sin \left (x+\displaystyle\frac{2\pi}{3}\right )\\ =\ &-\sin \left (x+\displaystyle\frac{\pi}{3}\right ).\end{aligned}\)
Tập xác định: \( \mathscr{D}=\mathbb{R}\).
\(\forall x \in \mathbb{R} \), ta có
\(\begin{aligned}-1 \leq -\sin \left (x+\displaystyle\frac{\pi}{3}\right ) \leq 1.\end{aligned}\)
\( \max y=1 \) khi \( \sin \left (x+\displaystyle\frac{\pi}{3}\right )=1 \Leftrightarrow x=\displaystyle\frac{\pi}{6}+k2\pi\).
\( \min y=-1 \) khi \( \sin \left (x+\displaystyle\frac{\pi}{3}\right )=-1 \Leftrightarrow x=-\displaystyle\frac{5\pi}{6}+k2\pi\).
Bài tập 8
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=\cos x+\cos (x+\pi / 3) \).
Áp dụng công thức \( \cos a+\cos b=2 \cos \displaystyle\frac{a+b}{2} \cos \displaystyle\frac{a-b}{2} \), ta có
\(\begin{aligned}y=\cos x+\cos \left (x+\displaystyle\frac{\pi}{3}\right )=\sqrt{3}\cos \left (x+\displaystyle\frac{\pi}{6}\right ).\end{aligned}\)
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&-1 \leq \cos \left (x+\displaystyle\frac{\pi}{6}\right ) \leq 1\\ \Leftrightarrow\ & -\sqrt{3} \leq \sqrt{3}\cos \left (x+\displaystyle\frac{\pi}{6}\right ) \leq \sqrt{3}.\end{aligned}\)
\( \max y=\sqrt{3} \) khi \( \cos \left (x+\displaystyle\frac{\pi}{6}\right ) =1 \Leftrightarrow x=-\displaystyle\frac{\pi}{6}+k2\pi\).
\( \min y=-\sqrt{3} \) khi \( \cos \left (x+\displaystyle\frac{\pi}{6}\right )=-1 \Leftrightarrow x=\displaystyle\frac{5\pi}{6}+k2\pi\).
Bài tập 9
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\displaystyle\frac{4}{2-\sin x}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \sin x\leq 1\\ \Leftrightarrow\ & -1\leq -\sin x\leq 1\\ \Leftrightarrow\ &1\leq 2-\sin x\leq 3\\ \Leftrightarrow\ & \displaystyle\frac{1}{3}\leq \displaystyle\frac{1}{2-\sin x}\leq 1\\ \Leftrightarrow\ & \displaystyle\frac{4}{3}\leq \displaystyle\frac{4}{2-\sin x}\leq 4.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=4\) khi \(x=\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=\displaystyle\frac{4}{3}\) khi \(x=-\displaystyle\frac{\pi}{2}\).
Bài tập 10
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\displaystyle\frac{8}{3-\cos ^{2} x}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& 0\leq \cos^2 x\leq 1\\ \Leftrightarrow\ & -1\leq -\cos^2 x\leq 0\\ \Leftrightarrow\ &2\leq 3-\cos^2 x\leq 3\\ \Leftrightarrow\ & \displaystyle\frac{8}{3}\leq \displaystyle\frac{8}{3-\cos^2 x}\leq 4.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=4\) khi \(x=0\) và \(\min\limits_{x \in \mathbb{R}} y=\displaystyle\frac{8}{3}\) khi \(x=\displaystyle\frac{\pi}{2}\).
Bài tập 11
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\displaystyle\frac{3}{3-\sqrt{1-\cos x}}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}&-1\leq \cos x\leq 1\\ \Leftrightarrow\ &-1\leq -\cos x\leq 1\\ \Leftrightarrow\ &0\leq \sqrt{1-\cos x}\leq \sqrt{2}\\ \Leftrightarrow\ &-\sqrt{2}\leq -\sqrt{1-\cos x}\leq 0\\ \Leftrightarrow\ &3-\sqrt{2}\leq 3 -\sqrt{1-\cos x}\leq 3\\ \Leftrightarrow\ &1\leq \displaystyle\frac{3}{3-\sqrt{1-\cos x}}\leq \displaystyle\frac{3}{3-\sqrt{2}}=\displaystyle\frac{9+3\sqrt{2}}{7}.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=\displaystyle\frac{9+3\sqrt{2}}{7}\) khi \(x=0\) và \(\min\limits_{x \in \mathbb{R}} y=1\) khi \(x=\pi\).
Bài tập 12
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\displaystyle\frac{1}{\sqrt{2-\sin ^{2} 3 x}}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& 0\leq \sin^2 3x\leq 1\\ \Leftrightarrow\ & -1\leq -\sin^2 3x\leq 0\\ \Leftrightarrow\ &1\leq 2-\sin^2 3x\leq 2\\ \Leftrightarrow\ &1\leq \sqrt{2-\sin^2 3x}\leq \sqrt{2}\\ \Leftrightarrow\ &\displaystyle\frac{1}{\sqrt{2}}\leq \displaystyle\frac{1}{\sqrt{2-\sin^2 3x}}\leq 1.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=1\) khi \(x=\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=\displaystyle\frac{\sqrt{2}}{2}\) khi \(x=0\).
Bài tập 13
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin x+\sqrt{3} \cos x+12\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi
\(\begin{aligned}y=\ &\sin x+\sqrt{3} \cos x+12\\ =\ &2\left(\displaystyle\frac{1}{2}\cdot\sin x+\displaystyle\frac{\sqrt{3}}{2}\cdot\cos x\right)+12\\ =\ &2\sin\left(x+\displaystyle\frac{\pi}{3}\right)+12.\end{aligned}\)
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}&-1\leq \sin\left(x+\displaystyle\frac{\pi}{3}\right)\leq 1\\ \Leftrightarrow\ & -2\leq 2\sin\left(x+\displaystyle\frac{\pi}{3}\right)\leq 2\\ \Leftrightarrow\ &10\leq 2\sin\left(x+\displaystyle\frac{\pi}{3}\right)+12\leq 14.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=14\) khi \(x=\displaystyle\frac{\pi}{6}\) và \(\min\limits_{x \in \mathbb{R}} y=10\) khi \(x=-\displaystyle\frac{5\pi}{6}\).
Bài tập 14
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{3} \sin x-\cos x+5\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi \(y=\sqrt{3} \sin x-\cos x+5=2\left(\displaystyle\frac{\sqrt{3}}{2}\cdot\sin x-\displaystyle\frac{1}{2}\cdot\cos x\right)+5=2\sin\left(x-\displaystyle\frac{\pi}{6}\right)+5\).\\
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \sin\left(x-\displaystyle\frac{\pi}{6}\right)\leq 1\\ \Leftrightarrow\ & -2\leq 2\sin\left(x-\displaystyle\frac{\pi}{6}\right)\leq 2\\ \Leftrightarrow\ &3\leq 2\sin\left(x-\displaystyle\frac{\pi}{6}\right)+5\leq 7.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=7\) khi \(x=\displaystyle\frac{2\pi}{3}\) và \(\min\limits_{x \in \mathbb{R}} y=3\) khi \(x=-\displaystyle\frac{\pi}{3}\).
Bài tập 15
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos 3x-\sqrt{3} \sin 3x+4\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi
\(\begin{aligned}y=\ &\cos 3x-\sqrt{3} \sin 3x+4\\ =\ &2\left(\displaystyle\frac{1}{2}\cdot\cos 3x -\displaystyle\frac{\sqrt{3}}{2}\cdot\sin 3x\right)+4\\ =\ &2\cos\left(3x+\displaystyle\frac{\pi}{3}\right)+4\end{aligned}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \cos\left(3x+\displaystyle\frac{\pi}{3}\right)\leq 1\\ \Leftrightarrow\ & -2\leq 2\cos\left(3x+\displaystyle\frac{\pi}{3}\right)\leq 2\\ \Leftrightarrow\ &2\leq 2\cos\left(3x+\displaystyle\frac{\pi}{3}\right)+4\leq 6.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=6\) khi \(x=-\displaystyle\frac{\pi}{9}\) và \(\min\limits_{x \in \mathbb{R}} y=2\) khi \(x=-\displaystyle\frac{4\pi}{9}\).
Bài tập 16
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{3}\left(\cos ^{4} x-\sin ^{4} x\right)+\sin 2 x+1\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi
\(\begin{aligned}y=& \sqrt{3}\left(\cos ^{2} x+\sin ^{2} x\right)\left(\cos ^{2} x-\sin ^{2} x\right)+\sin 2 x+1\\ =\ & \sqrt{3}\cos 2x+\sin 2 x+1\\ =\ & 2\left(\displaystyle\frac{\sqrt{3}}{2}\cdot\cos 2x +\displaystyle\frac{1}{2}\cdot\sin 2x\right)+1\\ =\ & 2\cos\left(2x-\displaystyle\frac{\pi}{6}\right)+1.\end{aligned}\)
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \cos\left(2x-\displaystyle\frac{\pi}{6}\right)\leq 1\\ \Leftrightarrow\ & -2\leq 2\cos\left(2x-\displaystyle\frac{\pi}{6}\right)\leq 2\\ \Leftrightarrow\ &-1\leq 2\cos\left(2x-\displaystyle\frac{\pi}{6}\right)+1\leq 3.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=3\) khi \(x=\displaystyle\frac{\pi}{12}\) và \(\min\limits_{x \in \mathbb{R}} y=-1\) khi \(x=\displaystyle\frac{7\pi}{12}\).
Bài tập 17
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=4 \sin ^{2} x-4 \sin x+3\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi \(y=4 \sin ^{2} x-4 \sin x+3=\left(2\sin x+1\right)^2+2\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \sin x\leq 1\\ \Leftrightarrow\ & -1\leq 2\sin x+1\leq 3\\ \Leftrightarrow\ &0\leq \left( 2\sin x+1\right)^2\leq 9\\ \Leftrightarrow\ &2\leq \left( 2\sin x+1\right)^2+2\leq 11.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=11\) khi \(x=\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=2\) khi \(\sin x=-\displaystyle\frac{1}{2}\).
Bài tập 18
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos ^{2} x-2 \cos x-4\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi \(y=\cos ^{2} x-2 \cos x-4=\left(\cos x-1\right)^2-5\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \cos x\leq 1\\ \Leftrightarrow\ & -2\leq \cos x-1\leq 0\\ \Leftrightarrow\ &0\leq \left( \cos x-1\right)^2\leq 4\\ \Leftrightarrow\ &-5\leq \left( \cos x-1\right)^2-5\leq -1.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=-1\) khi \(x=\pi\) và \(\min\limits_{x \in \mathbb{R}} y=-5\) khi \(x=0\).
Bài tập 19
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos ^{2} x+2 \sin x+2\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi \(y=\cos ^{2} x+2 \sin x+2=-\sin^2 x+2\sin x+3=-\left(\sin x-1\right)^2+4 \).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \sin x\leq 1\\ \Leftrightarrow\ & -2\leq \sin x-1\leq 0\\ \Leftrightarrow\ &0\leq \left( \sin x-1\right)^2\leq 4\\ \Leftrightarrow\ &-4\leq -\left( \sin x-1\right)^2\leq 0\\ \Leftrightarrow\ &0\leq -\left( \sin x-1\right)^2+4\leq 4.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=4\) khi \(x=\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=0\) khi \(x=-\displaystyle\frac{\pi}{2}\).
Bài tập 20
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos ^{4} x-2 \sin ^{2} x+1\) .
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi
\(\begin{aligned}y=\ &\cos ^{4} x-2 \sin ^{2} x+1\\ =\ &\cos ^{4} x-2 \left(1-\cos^2 x\right)+1\\ =\ &\cos ^{4} x+2 \cos ^{2} x-1\\ =\ &\left(\cos^2 x+1\right)^2-2\end{aligned}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& 0\leq \cos^2 x\leq 1\\ \Leftrightarrow\ & 1\leq \cos^2 x+1\leq 2\\ \Leftrightarrow\ &1\leq \left( \cos^2 x+1\right)^2\leq 4\\ \Leftrightarrow\ &-1\leq \left( \cos^2 x+1\right)^2-2\leq 2.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=2\) khi \(x=0\) và \(\min\limits_{x \in \mathbb{R}} y=-1\) khi \(x=\displaystyle\frac{\pi}{2}\).
Bài tập 21
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{5-4 \sin x+\sin ^{2} x}\).
Xét hàm số \(g(x)=5-4 \sin x+\sin ^{2} x\) trên \(\mathbb{R}\).
Ta có
\(g(x)=5-4 \sin x+\sin ^{2} x\) \(=\left(\sin x -2\right)^2+1\)
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& & -1\leq \sin x\leq 1\\ \Leftrightarrow\ &-3\leq \sin x-2\leq -1\\ \Leftrightarrow\ &1\leq \left( \sin x-2\right)^2\leq 9\\ \Leftrightarrow\ &2\leq \left( \sin x-2\right)^2+1\leq 10.\end{aligned}\)
Suy ra:
\(2\leq g(x)\leq 10 \Rightarrow \sqrt{2}\leq y\leq \sqrt{10}\).
Vậy \(\max\limits_{x \in \mathbb{R}} y=\sqrt{10}\) khi \(x=-\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=\sqrt{2}\) khi \(x=\displaystyle\frac{\pi}{2}\).
Bài tập 22
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{\cos ^{2} x+6 \cos x+14}\) .
Xét hàm số \(g(x)=\cos ^{2} x+6 \cos x+14\) trên \(\mathbb{R}\).
Ta có
\(g(x)=\cos ^{2} x+6 \cos x+14\) \(=\left(\cos x +3\right)^2+5\)
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \cos x\leq 1\\ \Leftrightarrow\ &2\leq \cos x+3\leq 4\\ \Leftrightarrow\ &4\leq \left( \cos x+3\right)^2\leq 16\\ \Leftrightarrow\ &9\leq \left( \cos x+3\right)^2+5\leq 21.\end{aligned}\)
Suy ra:
\(9\leq g(x)\leq 21 \Rightarrow 3\leq y\leq \sqrt{21}\).
Vậy \(\max\limits_{x \in \mathbb{R}} y=\sqrt{21}\) khi \(x=0\) và \(\min\limits_{x \in \mathbb{R}} y=3\) khi \(x=\pi\).
Bài tập 23
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=2(\sin x+\cos x)+\sin 2 x+3\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Đặt
\(t=\sin x+ \cos x=\sqrt{2}\sin \left(x+\displaystyle\frac{\pi}{4}\right)\), \(t\in \left[-\sqrt{2};\sqrt{2}\right]\).
Ta có
\(t^2=\left(\sin x+ \cos x\right)^2\) \(=1+2\sin x\cos x=1+\sin 2x\) \(\Rightarrow \sin 2x =t^2-1\).
Hàm số trở thành \(y=g(t)=t^2+2t+2\).
Bảng biến thiên của hàm số \(y=g(t)\) trên đoạn \( \left[-\sqrt{2};\sqrt{2}\right]\)

Vậy \(\max\limits_{x \in \mathbb{R}} y=4+2\sqrt{2}\) và \(\min\limits_{x \in \mathbb{R}} y=1\).
Bài tập 24
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin x+\cos x+2 \sin x \cos x-1\) .
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Đặt \(t=\sin x+ \cos x=\sqrt{2}\sin \left(x+\displaystyle\frac{\pi}{4}\right)\), \(t\in \left[-\sqrt{2};\sqrt{2}\right]\).
Ta có
\(t^2=\left(\sin x+ \cos x\right)^2=1+2\sin x\cos x\) \(\Rightarrow 2\sin x\cos x =t^2-1\).
Hàm số trở thành \(y=g(t)=t^2+t-2\). \\
Bảng biến thiên của hàm số \(y=g(t)\) trên đoạn \( \left[-\sqrt{2};\sqrt{2}\right]\)

Vậy \(\max\limits_{x \in \mathbb{R}} y=\sqrt{2}\) và \(\min\limits_{x \in \mathbb{R}} y=-\displaystyle\frac{9}{4}\).
Bài tập 25
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=3-\sin 2 x\) trên đoạn \(\left[ 0; \displaystyle\frac{\pi}{2}\right]\)?
Ta có
\(x\in \left[ 0; \displaystyle\frac{\pi}{2}\right]\Rightarrow 2x\in \left[ 0; \pi\right]\).

Với mọi \(2x\in \left[ 0; \pi\right]\) ta có
\(\begin{aligned}& 0\leq \sin 2x\leq 1\\ \Leftrightarrow\ & -1\leq -\sin 2x\leq 0\\ \Leftrightarrow\ &2\leq 3-\sin 2x\leq 3.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[ 0; \tfrac{\pi}{2}\right]} y=3\) khi \(x=0\) và \(\min\limits_{x \in \left[ 0; \tfrac{\pi}{2}\right]} y=2\) khi \(x=\displaystyle\frac{\pi}{4}\).
Bài tập 26
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin 2 x+2\) trên \(\left[ 0; \displaystyle\frac{\pi}{2}\right]\)?
Ta có \(x\in \left[ 0; \displaystyle\frac{\pi}{2}\right]\Rightarrow 2x\in \left[ 0; \pi\right]\).

Với mọi \(2x\in \left[ 0; \pi\right]\) ta có
\(\begin{aligned}& 0\leq \sin 2x\leq 1\\ \Leftrightarrow\ &2\leq \sin 2x+2\leq 3.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[ 0; \tfrac{\pi}{2}\right]} y=3\) khi \(x=\displaystyle\frac{\pi}{4}\) và \(\min\limits_{x \in \left[ 0; \tfrac{\pi}{2}\right]} y=2\) khi \(x=0\).
Bài tập 27
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos \left(x+\displaystyle\frac{\pi}{3}\right)\) trên \([0 ; \pi]\).
Ta có
\(x\in \left[ 0; \pi\right]\) \(\Rightarrow x+\displaystyle\frac{\pi}{3}\in \left[ \displaystyle\frac{\pi}{3}; \displaystyle\frac{4\pi}{3}\right]\).

Do đó: \( -1 \leq \cos \left(x+\displaystyle\frac{\pi}{3}\right)\leq \displaystyle\frac{1}{2}\).
Vậy \(\max\limits_{x \in [0 ; \pi]} y=\displaystyle\frac{1}{2}\) khi \(x=0\) và \(\min\limits_{x \in [0 ; \pi]} y=-1\) khi \(x=\displaystyle\frac{2\pi}{3}\).
Bài tập 28
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin \left(2 x+\displaystyle\frac{\pi}{4}\right)+\displaystyle\frac{1}{2}\) trên \(\left[-\displaystyle\frac{\pi}{4} ; \displaystyle\frac{\pi}{4}\right]\).
Ta có \(x\in \left[ -\displaystyle\frac{\pi}{4}; \displaystyle\frac{\pi}{4}\right]\) \(\Rightarrow 2x+\displaystyle\frac{\pi}{4}\in \left[-\displaystyle\frac{\pi}{4}; \displaystyle\frac{3\pi}{4}\right]\).

Do đó:
\(\begin{aligned}& -\displaystyle\frac{\sqrt{2}}{2}\leq \sin \left(2 x+\displaystyle\frac{\pi}{4}\right)\leq 1\\ \Rightarrow\ & \displaystyle\frac{1-\sqrt{2}}{2}\leq \sin \left(2 x+\displaystyle\frac{\pi}{4}\right)+\displaystyle\frac{1}{2}\leq \displaystyle\frac{3}{2}.\end{aligned}\)
Vậy \(\max\limits_{x \in\left[-\tfrac{\pi}{4} ; \tfrac{\pi}{4}\right]} y=\displaystyle\frac{3}{2}\) và \(\min\limits_{x \in \left[-\tfrac{\pi}{4} ; \tfrac{\pi}{4}\right]} y=\displaystyle\frac{1-\sqrt{2}}{2}\).
Bài tập 29
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin^4 x+\cos^4 x-1\) = trên \(\left[0 ; \displaystyle\frac{\pi}{6}\right]\).
Ta có
\(\begin{aligned}&\sin^4 x+\cos^4 x\\ =\ & \left(\sin^2 x+\cos^2 x\right)^2-2\sin^2 x\cdot \cos^2 x\\ =\ &1-\displaystyle\frac{1}{2}\sin^2 2x\\ =\ &1-\displaystyle\frac{1-\cos 4x}{4}\\ =\ &\displaystyle\frac{3}{4}+\displaystyle\frac{1}{4}\cos 4x.\end{aligned}\)
Suy ra:
\(y=\sin^4 x+\cos^4 x-1=\displaystyle\frac{1}{4}\cos 4x-\displaystyle\frac{1}{4}\).

Do \(x\in \left[ 0 ; \displaystyle\frac{\pi}{6}\right]\Rightarrow 4x \in \left[0; \displaystyle\frac{2\pi}{3}\right]\).
Do đó:
\(\begin{aligned}& -\displaystyle\frac{1}{2}\leq\cos 4x \leq 1\\ \Leftrightarrow\ & -\displaystyle\frac{1}{8}\leq \displaystyle\frac{1}{4}\cos 4x \leq \displaystyle\frac{1}{4}\\ \Leftrightarrow\ & -\displaystyle\frac{3}{8}\leq \displaystyle\frac{1}{4}\cos 4x-\displaystyle\frac{1}{4} \leq 0.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[0 ; \tfrac{\pi}{6}\right]} y=0\) và \(\min\limits_{x \in \left[0 ; \tfrac{\pi}{6}\right]} y=-\displaystyle\frac{3}{8}\).
Bài tập 30
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin^6 x+\cos^6 x\) trên \(\left[-\displaystyle\frac{\pi}{2} ; \displaystyle\frac{\pi}{2}\right]\).
Ta có
\(\begin{aligned}&\sin^6 x+\cos^6 x\\ =\ & \left(\sin^2 x+\cos^2 x\right)^3-3\sin^2 x\cdot \cos^2 x\left(\sin^2 x+\cos^2 x \right)\\ =\ &1-\displaystyle\frac{3}{4}\sin^2 2x\\ =\ &1-\displaystyle\frac{3}{4}\cdot \displaystyle\frac{1-\cos 4x}{2}\\ =\ &\displaystyle\frac{5}{8}+\displaystyle\frac{3}{8}\cos 4x.\end{aligned}\)
Suy ra:
\(y=\sin^6 x+\cos^6 x = \displaystyle\frac{5}{8}+\displaystyle\frac{3}{8}\cos 4x\).
Do \(x\in \left[-\displaystyle\frac{\pi}{2} ; \displaystyle\frac{\pi}{2} \right]\Rightarrow 4x \in \left[-2\pi ; 2\pi\right]\) nên
\(\begin{aligned}& -1\leq\cos 4x \leq 1\\ \Leftrightarrow\ & -\displaystyle\frac{3}{8}\leq \displaystyle\frac{3}{8}\cos 4x \leq \displaystyle\frac{3}{8}\\ \Leftrightarrow\ & \displaystyle\frac{1}{4}\leq \displaystyle\frac{5}{8}+ \displaystyle\frac{3}{8}\cos 4x \leq 1.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[-\tfrac{\pi}{2} ; \tfrac{\pi}{2}\right]} y=1\) và \(\min\limits_{x \in \left[-\tfrac{\pi}{2} ; \tfrac{\pi}{2}\right]} y=\displaystyle\frac{1}{4}\).
Bài tập 31
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{3} \sin 2 x+2 \cos^2 x+3\) trên \(\left[-\displaystyle\frac{5 \pi}{6}; \displaystyle\frac{\pi}{4}\right]\).
Ta có
\(\begin{aligned}y=\ & \sqrt{3} \sin 2 x+2 \cos^2 x+3\\ =\ &\sqrt{3} \sin 2 x+2\cdot\displaystyle\frac{1+\cos 2x}{2}+3\\ =\ & \sqrt{3} \sin 2 x+\cos 2x+4\\ =\ &2\sin \left(2x+\displaystyle\frac{\pi}{6}\right)+4.\end{aligned}\)
Do \(x\in \left[-\displaystyle\frac{5 \pi}{6}; \displaystyle\frac{\pi}{4}\right]\) \(\Rightarrow 2x \in \left[-\displaystyle\frac{5 \pi}{3}; \displaystyle\frac{\pi}{2}\right]\) \(\Rightarrow 2x +\displaystyle\frac{\pi}{6}\in \left[-\displaystyle\frac{3\pi}{2}; \displaystyle\frac{2\pi}{3}\right]\) .
Do đó:
\(\begin{aligned}& -1\leq \sin \left(2x+\displaystyle\frac{\pi}{6}\right) \leq 1\\ \Leftrightarrow\ & -2\leq 2\sin \left(2x+\displaystyle\frac{\pi}{6}\right) \leq 2\\ \Leftrightarrow\ & 2\leq 2\sin \left(2x+\displaystyle\frac{\pi}{6}\right)+4 \leq 6.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[-\tfrac{5 \pi}{6}; \tfrac{\pi}{4}\right]} y=6\) và \(\min\limits_{x \in \left[-\tfrac{5 \pi}{6}; \tfrac{\pi}{4}\right]} y=2\).
Bài tập 32
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin 2 x+\cos 2 x+3\) trên \(\left[-\displaystyle\frac{\pi}{4} ; \displaystyle\frac{\pi}{4}\right]\).
Ta có \(y= \sin 2 x+\cos 2 x+3= \sqrt{2}\sin \left(2x+\displaystyle\frac{\pi}{4}\right)+3\).
Do \(x\in \left[-\displaystyle\frac{\pi}{4} ; \displaystyle\frac{\pi}{4}\right]\Rightarrow 2x \in \left[-\displaystyle\frac{\pi}{2} ; \displaystyle\frac{\pi}{2}\right]\) \(\Rightarrow 2x +\displaystyle\frac{\pi}{4}\in \left[-\displaystyle\frac{\pi}{4}; \displaystyle\frac{3\pi}{4}\right]\).

Do đó:
\(\begin{aligned}& -\displaystyle\frac{\sqrt{2}}{2}\leq\sin \left(2x+\displaystyle\frac{\pi}{4}\right) \leq 1\\ \Leftrightarrow\ & -1\leq \sqrt{2} \sin \left(2x+\displaystyle\frac{\pi}{4}\right)\leq \sqrt{2}\\ \Leftrightarrow\ & 2\leq \sqrt{2}\sin \left(2x+\displaystyle\frac{\pi}{4}\right)+3 \leq 3+\sqrt{2}.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[-\tfrac{\pi}{4} ; \tfrac{\pi}{4}\right]} y=3+\sqrt{2}\) và \(\min\limits_{x \in \left[-\tfrac{\pi}{4} ; \tfrac{\pi}{4}\right]} y=2\).
Dạng 3. Xét tính chẵn lẻ của hàm số lượng giác
Phương pháp giải
Bài tập 1
Xét tính chẵn, lẻ của hàm số \(f(x)=\sin^2 2x+\cos 3x\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\sin^2(-2x)+\cos(-3x)\) \(=\sin^2 2x+\cos 3x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 2
Xét tính chẵn, lẻ của hàm số \(f(x)=\cos^2 3x+\cos x\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\cos^2(-3x)+\cos(-x)\) \(=\cos^2 3x+\cos x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 3
Xét tính chẵn, lẻ của hàm số \(f(x)=\displaystyle\frac{\sin^2 x-\cos x}{\sin 3x}\).
Điều kiện xác định \(\sin 3x\ne0\Leftrightarrow x\ne\displaystyle\frac{k\pi}{3}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{3},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\displaystyle\frac{\sin^2(-x)-\cos(-x)}{\sin(-3x)}\) \(=\displaystyle\frac{\sin^2 x-\cos x}{-\sin 3x}=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Bài tập 4
Xét tính chẵn, lẻ của hàm số \(f(x)=1+\cos x\cdot\sin\left(\displaystyle\frac{3\pi}{2}-2x\right)\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(x)=1+\cos x\cdot\sin\left(\displaystyle\frac{3\pi}{2}-2x\right)\) \(=1-\cos x\cdot\sin\left(\displaystyle\frac{\pi}{2}-2x\right)\) \(=1-\cos x\cdot\cos 2x\).
Khi đó
\(f(-x)=1-\cos(-x)\cdot\cos(-2x)\) \(=1-\cos x\cdot\cos 2x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 5
Xét tính chẵn, lẻ của hàm số \(f(x)=\cos\sqrt{x^2-16}\).
Điều kiện xác định của hàm số là \(x^2-16\ge0\Leftrightarrow\left[\begin{aligned}x\ge4\\ x\le-4.\end{aligned}\right.\)
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus(-4;4)\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\cos\sqrt{(-x)^2-16}\) \(=\cos\sqrt{x^2-16}=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 6
Xét tính chẵn, lẻ của hàm số \(f(x)=\tan x+\cot x\).
Điều kiện xác định của hàm số là \(\begin{cases}\sin x\ne0\\ \cos x\ne0\end{cases}\Leftrightarrow x\ne\displaystyle\frac{k\pi}{2}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{2},\ k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\tan(-x)+\cot(-x)\) \(=-\tan x-\cot x=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Bài tập 7
Xét tính chẵn, lẻ của hàm số \(f(x)=\cot(4x+5\pi)\cdot\tan(2x-3\pi)\).
Ta có
\(f(x)=\cot(4x+5\pi)\cdot\tan(2x-3\pi)\) \(=\cot 4x\cdot\tan 2x\).
Điều kiện xác định của hàm số là
\(\begin{cases}\sin 4x\ne0\\ \cos 2x\ne0\end{cases}\) \(\Leftrightarrow\begin{cases}x\ne\displaystyle\frac{k\pi}{4}\\ x\ne\displaystyle\frac{\pi}{4}+\displaystyle\frac{k\pi}{2}\end{cases}\) \(\Leftrightarrow x\ne\displaystyle\frac{k\pi}{4}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{4},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\cot(-4x)\cdot\tan(-2x)\) \(=\cot 4x\cdot\tan 2x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 8
Xét tính chẵn, lẻ của hàm số \(f(x)=\sin^3(3x+\pi)+\cot(2x-7\pi)\).
Ta có
\(f(x)=\sin^3(3x+\pi)+\cot(2x-7\pi)\) \(=-\sin^3 x+\cot 2x\).
Điều kiện xác định của hàm số là \(\sin 2x\ne0\Leftrightarrow x\ne\displaystyle\frac{k\pi}{2}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{2},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=-\sin^3(-x)+\cot(-2x)\) \(=\sin^3 x-\cot 2x=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Bài tập 9
Xét tính chẵn, lẻ của hàm số \(f(x)=\left|\sin x-\displaystyle\frac{1}{2}\right|+\left|\sin x+\displaystyle\frac{1}{2}\right|\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng. Ta có
\(\begin{aligned}f(-x)=\ &\left|\sin (-x)-\displaystyle\frac{1}{2}\right|+\left|\sin (-x)+\displaystyle\frac{1}{2}\right|\\ =\ &\left|-\sin x-\displaystyle\frac{1}{2}\right|+\left|-\sin x+\displaystyle\frac{1}{2}\right|\\ =\ &\left|\sin x+\displaystyle\frac{1}{2}\right|+\left|\sin x-\displaystyle\frac{1}{2}\right|\\ =\ &f(x),\,\forall x\in\mathscr{D}.\end{aligned}\)
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 10
Xét tính chẵn, lẻ của hàm số \(f(x)=\displaystyle\frac{\sqrt{\cos x+2}+\cot^2 x}{\sin 4x}\).
Điều kiện xác định
\(\begin{cases}\cos x+2\ge 0\\ \sin x\ne 0\\ \sin 4x\ne 0\end{cases}\) \(\Leftrightarrow\begin{cases}\cos x\ge -2\\ \sin 4x\ne 0\end{cases}\) \(\Leftrightarrow 4x\ne k\pi\) \(\Leftrightarrow x\ne\displaystyle\frac{k\pi}{4}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{4},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\displaystyle\frac{\sqrt{\cos(-x)+2}+\cot^2(-x)}{\sin(-4x)}\) \(=\displaystyle\frac{\sqrt{\cos x+2}+\cot^2 x}{-\sin 4x}=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Dạng 4. Tìm chu kì của hàm số lượng giác
Phương pháp giải
Bài tập 1
Hàm số \(y=\sin 2x\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=2\pi\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=\pi\)
D. \(T_0=4\pi\)
Ta có hàm số \(y=\sin 2x\) tuần hoàn với chu kỳ \(T_0=\displaystyle\frac{2\pi}{2}=\pi\).
Bài tập 2
Hàm số \(y=\tan 2x\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=\displaystyle\frac{\pi}{3}\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=2\pi\)
D. \(T_0=\pi\)
Ta có hàm số \(y=\tan 2x\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{\pi}{2}\).
Bài tập 3
Hàm số \(y=3\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=0\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=2\pi\)
D. \(T_0=4\pi\)
Ta có hàm số \(y=3\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{2\pi}{\tfrac{1}{2}}=4\pi\).
Bài tập 4
Hàm số \(f(x)=\sin\displaystyle\frac{x}{2}+2\cos\displaystyle\frac{3x}{2}\) tuần hoàn với chu kỳ chu kỳ là
A. \(5\pi\)
B. \(\displaystyle\frac{\pi}{2}\)
C. \(3\pi\)
D. \(4\pi\)
Ta có
+) hàm số \(\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ \(T_1=\displaystyle\frac{2\pi}{\tfrac{1}{2}}=4\pi\),
+) hàm số \(\cos\displaystyle\frac{3x}{2}\) tuần hoàn với chu kỳ \(T_2=\displaystyle\frac{2\pi}{\tfrac{3}{2}}=\displaystyle\frac{4\pi}{3}\).
Do đó hàm số \(f(x)\) tuần hoàn với chu kỳ \(T_0\) là bội chung nhỏ nhất của \(T_1\) và \(T_2\).
Do \(T_1\) là bội của \(T_2\) \(\left(\displaystyle\frac{T_1}{T_2}=3\right)\) nên \(T_0=T_1\).
Vậy hàm số \(f(x)\) đã cho tuần hoàn với chu kỳ \(T_0=4\pi\).
Bài tập 5
Tìm \(m\) để hàm số \(y=\cos mx\) tuần hoàn với chu kỳ \(T_0=\pi\).
A. \(m=\pm1\)
B. \(m=\pm2\)
C. \(m=\pm\displaystyle\frac{\pi}{2}\)
D. \(m=\pm\pi\)
Ta có hàm số \(y=\cos mx\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{2\pi}{|m|}\).
Để hàm số tuần hoàn với chu kỳ \(T_0=\pi\) thì
\(T=T_0\Leftrightarrow \displaystyle\frac{2\pi}{|m|}=\pi\Leftrightarrow |m|=2\Leftrightarrow m=\pm2\).
Bài tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=5-3 \cos 4 x \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&-1 \leq \cos 4 x \leq 1 \\\Leftrightarrow\ & 3 \geq-3 \cos 4 x \geq-3\\ \Leftrightarrow\ & 5+3 \geq 5-3 \cos 4 x \geq 5-3 \\ \Leftrightarrow\ & 2 \leq y \leq 8.\end{aligned}\)
\(\max y=8\) khi
\(\cos 4 x=-1 \Leftrightarrow x=\displaystyle\frac{\pi}{4}+\displaystyle\frac{k\pi}{2}\).
\(\min y=2\) khi
\(\cos 4 x=1 \Leftrightarrow x=\displaystyle\frac{k\pi}{2}\).
Bài tập 2
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=2+3 \cos x \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&-1 \leq \cos x \leq 1\\\Leftrightarrow\ & -3 \geq3 \cos x \geq-3\\ \Leftrightarrow\ &-1 \geq 2+3 \cos x \geq 5\\ \Leftrightarrow\ & -1 \leq y \leq 5. \end{aligned}\)
\(\max y=5 \) khi \( \cos x=1 \Leftrightarrow x=k2\pi\).
\( \min y=-1 \) khi \( \cos x=-1 \Leftrightarrow x=\pi +k2\pi\).
Bài tập 3
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=3-2 \sin 2 x \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&-1 \leq \sin 2x \leq 1\\ \Leftrightarrow\ & -2 \leq -2\sin 2x \leq 2\\ \Leftrightarrow\ & 1 \leq 3-2\sin 2x \leq 5\\ \Leftrightarrow\ & 1 \leq y \leq 5.\end{aligned}\)
\( \max y=5 \) khi \( \sin 2x=-1 \Leftrightarrow x=-\displaystyle\frac{\pi}{4}+k\pi\).
\( \min y=1 \) khi \( \sin 2x=1 \Leftrightarrow x=\displaystyle\frac{\pi}{4}+k\pi\).
Bài tập 4
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=3-2|\sin 2 x| \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&0\leq |\sin 2 x|\leq 1\\ \Leftrightarrow\ & -2\leq -2|\sin 2 x|\leq 0\\ \Leftrightarrow\ & 1\leq 3-2|\sin 2 x|\leq 3.\end{aligned}\)
\( \max y=3 \) khi \( \sin 2 x=0 \Leftrightarrow x=\displaystyle\frac{k\pi}{2}\).
\( \min y=1\) khi \( \sin 2 x=\pm1 \Leftrightarrow x=\displaystyle\frac{\pm\pi}{4}+k\pi\).
Bài tập 5
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=\displaystyle\frac{1+4 \cos ^{2} x}{3} \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}& 0\leq \cos ^{2} x \leq 1\\ \Leftrightarrow\ & 0\leq 4\cos ^{2} x \leq 4\\ \Leftrightarrow\ & 1\leq 1+4\cos ^{2} x \leq5\\ \Leftrightarrow\ & \displaystyle\frac{1}{3}\leq \displaystyle\frac{1+4\cos ^{2} x}{3} \leq \displaystyle\frac{5}{3}.\end{aligned}\)
\( \max y=\displaystyle\frac{5}{3} \) khi \( \cos x=0 \Leftrightarrow x=\displaystyle\frac{\pi}{2}+k\pi\).
\( \min y=\displaystyle\frac{1}{3} \) khi \( \cos x=\pm1 \Leftrightarrow x=k\pi\).
Bài tập 6
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=1-\displaystyle\frac{1}{2} \sin ^{2} 2 x \).
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}& 0 \leq \sin ^{2} 2 x \leq 1\\ \Leftrightarrow\ & -\displaystyle\frac{1}{2} \leq -\displaystyle\frac{1}{2}\cdot\sin ^{2} 2 x \leq 0\\ \Leftrightarrow\ & \displaystyle\frac{1}{2} \leq -\displaystyle\frac{1}{2}\cdot\sin ^{2} 2 x \leq 1.\end{aligned}\)
\( \max y=1 \) khi \( \sin 2 x=0 \Leftrightarrow x=\displaystyle\frac{\pi}{4}+\displaystyle\frac{k\pi}{2}\).
\( \min y=\displaystyle\frac{1}{2} \) khi \( \sin 2 x=\pm1 \Leftrightarrow x=\displaystyle\frac{\pi}{4}+\displaystyle\frac{k\pi}{2}\).
Bài tập 7
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=\sin x+\sin (x+2 \pi / 3) \).
Áp dụng công thức \fbox\( \sin a+\sin b=2 \sin \displaystyle\frac{a+b}{2} \cos \displaystyle\frac{a-b}{2} \), ta có
\(\begin{aligned}y=\ &\sin x + \sin \left (x+\displaystyle\frac{2\pi}{3}\right )\\ =\ &-\sin \left (x+\displaystyle\frac{\pi}{3}\right ).\end{aligned}\)
Tập xác định: \( \mathscr{D}=\mathbb{R}\).
\(\forall x \in \mathbb{R} \), ta có
\(\begin{aligned}-1 \leq -\sin \left (x+\displaystyle\frac{\pi}{3}\right ) \leq 1.\end{aligned}\)
\( \max y=1 \) khi \( \sin \left (x+\displaystyle\frac{\pi}{3}\right )=1 \Leftrightarrow x=\displaystyle\frac{\pi}{6}+k2\pi\).
\( \min y=-1 \) khi \( \sin \left (x+\displaystyle\frac{\pi}{3}\right )=-1 \Leftrightarrow x=-\displaystyle\frac{5\pi}{6}+k2\pi\).
Bài tập 8
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y=\cos x+\cos (x+\pi / 3) \).
Áp dụng công thức \( \cos a+\cos b=2 \cos \displaystyle\frac{a+b}{2} \cos \displaystyle\frac{a-b}{2} \), ta có
\(\begin{aligned}y=\cos x+\cos \left (x+\displaystyle\frac{\pi}{3}\right )=\sqrt{3}\cos \left (x+\displaystyle\frac{\pi}{6}\right ).\end{aligned}\)
Tập xác định: \( \mathscr{D}=\mathbb{R}\). \( \forall x \in \mathbb{R} \), ta có
\(\begin{aligned}&-1 \leq \cos \left (x+\displaystyle\frac{\pi}{6}\right ) \leq 1\\ \Leftrightarrow\ & -\sqrt{3} \leq \sqrt{3}\cos \left (x+\displaystyle\frac{\pi}{6}\right ) \leq \sqrt{3}.\end{aligned}\)
\( \max y=\sqrt{3} \) khi \( \cos \left (x+\displaystyle\frac{\pi}{6}\right ) =1 \Leftrightarrow x=-\displaystyle\frac{\pi}{6}+k2\pi\).
\( \min y=-\sqrt{3} \) khi \( \cos \left (x+\displaystyle\frac{\pi}{6}\right )=-1 \Leftrightarrow x=\displaystyle\frac{5\pi}{6}+k2\pi\).
Bài tập 9
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\displaystyle\frac{4}{2-\sin x}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \sin x\leq 1\\ \Leftrightarrow\ & -1\leq -\sin x\leq 1\\ \Leftrightarrow\ &1\leq 2-\sin x\leq 3\\ \Leftrightarrow\ & \displaystyle\frac{1}{3}\leq \displaystyle\frac{1}{2-\sin x}\leq 1\\ \Leftrightarrow\ & \displaystyle\frac{4}{3}\leq \displaystyle\frac{4}{2-\sin x}\leq 4.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=4\) khi \(x=\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=\displaystyle\frac{4}{3}\) khi \(x=-\displaystyle\frac{\pi}{2}\).
Bài tập 10
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\displaystyle\frac{8}{3-\cos ^{2} x}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& 0\leq \cos^2 x\leq 1\\ \Leftrightarrow\ & -1\leq -\cos^2 x\leq 0\\ \Leftrightarrow\ &2\leq 3-\cos^2 x\leq 3\\ \Leftrightarrow\ & \displaystyle\frac{8}{3}\leq \displaystyle\frac{8}{3-\cos^2 x}\leq 4.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=4\) khi \(x=0\) và \(\min\limits_{x \in \mathbb{R}} y=\displaystyle\frac{8}{3}\) khi \(x=\displaystyle\frac{\pi}{2}\).
Bài tập 11
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\displaystyle\frac{3}{3-\sqrt{1-\cos x}}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}&-1\leq \cos x\leq 1\\ \Leftrightarrow\ &-1\leq -\cos x\leq 1\\ \Leftrightarrow\ &0\leq \sqrt{1-\cos x}\leq \sqrt{2}\\ \Leftrightarrow\ &-\sqrt{2}\leq -\sqrt{1-\cos x}\leq 0\\ \Leftrightarrow\ &3-\sqrt{2}\leq 3 -\sqrt{1-\cos x}\leq 3\\ \Leftrightarrow\ &1\leq \displaystyle\frac{3}{3-\sqrt{1-\cos x}}\leq \displaystyle\frac{3}{3-\sqrt{2}}=\displaystyle\frac{9+3\sqrt{2}}{7}.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=\displaystyle\frac{9+3\sqrt{2}}{7}\) khi \(x=0\) và \(\min\limits_{x \in \mathbb{R}} y=1\) khi \(x=\pi\).
Bài tập 12
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\displaystyle\frac{1}{\sqrt{2-\sin ^{2} 3 x}}\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& 0\leq \sin^2 3x\leq 1\\ \Leftrightarrow\ & -1\leq -\sin^2 3x\leq 0\\ \Leftrightarrow\ &1\leq 2-\sin^2 3x\leq 2\\ \Leftrightarrow\ &1\leq \sqrt{2-\sin^2 3x}\leq \sqrt{2}\\ \Leftrightarrow\ &\displaystyle\frac{1}{\sqrt{2}}\leq \displaystyle\frac{1}{\sqrt{2-\sin^2 3x}}\leq 1.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=1\) khi \(x=\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=\displaystyle\frac{\sqrt{2}}{2}\) khi \(x=0\).
Bài tập 13
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin x+\sqrt{3} \cos x+12\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi
\(\begin{aligned}y=\ &\sin x+\sqrt{3} \cos x+12\\ =\ &2\left(\displaystyle\frac{1}{2}\cdot\sin x+\displaystyle\frac{\sqrt{3}}{2}\cdot\cos x\right)+12\\ =\ &2\sin\left(x+\displaystyle\frac{\pi}{3}\right)+12.\end{aligned}\)
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}&-1\leq \sin\left(x+\displaystyle\frac{\pi}{3}\right)\leq 1\\ \Leftrightarrow\ & -2\leq 2\sin\left(x+\displaystyle\frac{\pi}{3}\right)\leq 2\\ \Leftrightarrow\ &10\leq 2\sin\left(x+\displaystyle\frac{\pi}{3}\right)+12\leq 14.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=14\) khi \(x=\displaystyle\frac{\pi}{6}\) và \(\min\limits_{x \in \mathbb{R}} y=10\) khi \(x=-\displaystyle\frac{5\pi}{6}\).
Bài tập 14
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{3} \sin x-\cos x+5\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi \(y=\sqrt{3} \sin x-\cos x+5=2\left(\displaystyle\frac{\sqrt{3}}{2}\cdot\sin x-\displaystyle\frac{1}{2}\cdot\cos x\right)+5=2\sin\left(x-\displaystyle\frac{\pi}{6}\right)+5\).\\
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \sin\left(x-\displaystyle\frac{\pi}{6}\right)\leq 1\\ \Leftrightarrow\ & -2\leq 2\sin\left(x-\displaystyle\frac{\pi}{6}\right)\leq 2\\ \Leftrightarrow\ &3\leq 2\sin\left(x-\displaystyle\frac{\pi}{6}\right)+5\leq 7.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=7\) khi \(x=\displaystyle\frac{2\pi}{3}\) và \(\min\limits_{x \in \mathbb{R}} y=3\) khi \(x=-\displaystyle\frac{\pi}{3}\).
Bài tập 15
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos 3x-\sqrt{3} \sin 3x+4\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi
\(\begin{aligned}y=\ &\cos 3x-\sqrt{3} \sin 3x+4\\ =\ &2\left(\displaystyle\frac{1}{2}\cdot\cos 3x -\displaystyle\frac{\sqrt{3}}{2}\cdot\sin 3x\right)+4\\ =\ &2\cos\left(3x+\displaystyle\frac{\pi}{3}\right)+4\end{aligned}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \cos\left(3x+\displaystyle\frac{\pi}{3}\right)\leq 1\\ \Leftrightarrow\ & -2\leq 2\cos\left(3x+\displaystyle\frac{\pi}{3}\right)\leq 2\\ \Leftrightarrow\ &2\leq 2\cos\left(3x+\displaystyle\frac{\pi}{3}\right)+4\leq 6.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=6\) khi \(x=-\displaystyle\frac{\pi}{9}\) và \(\min\limits_{x \in \mathbb{R}} y=2\) khi \(x=-\displaystyle\frac{4\pi}{9}\).
Bài tập 16
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{3}\left(\cos ^{4} x-\sin ^{4} x\right)+\sin 2 x+1\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi
\(\begin{aligned}y=& \sqrt{3}\left(\cos ^{2} x+\sin ^{2} x\right)\left(\cos ^{2} x-\sin ^{2} x\right)+\sin 2 x+1\\ =\ & \sqrt{3}\cos 2x+\sin 2 x+1\\ =\ & 2\left(\displaystyle\frac{\sqrt{3}}{2}\cdot\cos 2x +\displaystyle\frac{1}{2}\cdot\sin 2x\right)+1\\ =\ & 2\cos\left(2x-\displaystyle\frac{\pi}{6}\right)+1.\end{aligned}\)
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \cos\left(2x-\displaystyle\frac{\pi}{6}\right)\leq 1\\ \Leftrightarrow\ & -2\leq 2\cos\left(2x-\displaystyle\frac{\pi}{6}\right)\leq 2\\ \Leftrightarrow\ &-1\leq 2\cos\left(2x-\displaystyle\frac{\pi}{6}\right)+1\leq 3.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=3\) khi \(x=\displaystyle\frac{\pi}{12}\) và \(\min\limits_{x \in \mathbb{R}} y=-1\) khi \(x=\displaystyle\frac{7\pi}{12}\).
Bài tập 17
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=4 \sin ^{2} x-4 \sin x+3\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi \(y=4 \sin ^{2} x-4 \sin x+3=\left(2\sin x+1\right)^2+2\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \sin x\leq 1\\ \Leftrightarrow\ & -1\leq 2\sin x+1\leq 3\\ \Leftrightarrow\ &0\leq \left( 2\sin x+1\right)^2\leq 9\\ \Leftrightarrow\ &2\leq \left( 2\sin x+1\right)^2+2\leq 11.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=11\) khi \(x=\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=2\) khi \(\sin x=-\displaystyle\frac{1}{2}\).
Bài tập 18
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos ^{2} x-2 \cos x-4\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi \(y=\cos ^{2} x-2 \cos x-4=\left(\cos x-1\right)^2-5\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \cos x\leq 1\\ \Leftrightarrow\ & -2\leq \cos x-1\leq 0\\ \Leftrightarrow\ &0\leq \left( \cos x-1\right)^2\leq 4\\ \Leftrightarrow\ &-5\leq \left( \cos x-1\right)^2-5\leq -1.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=-1\) khi \(x=\pi\) và \(\min\limits_{x \in \mathbb{R}} y=-5\) khi \(x=0\).
Bài tập 19
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos ^{2} x+2 \sin x+2\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi \(y=\cos ^{2} x+2 \sin x+2=-\sin^2 x+2\sin x+3=-\left(\sin x-1\right)^2+4 \).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \sin x\leq 1\\ \Leftrightarrow\ & -2\leq \sin x-1\leq 0\\ \Leftrightarrow\ &0\leq \left( \sin x-1\right)^2\leq 4\\ \Leftrightarrow\ &-4\leq -\left( \sin x-1\right)^2\leq 0\\ \Leftrightarrow\ &0\leq -\left( \sin x-1\right)^2+4\leq 4.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=4\) khi \(x=\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=0\) khi \(x=-\displaystyle\frac{\pi}{2}\).
Bài tập 20
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos ^{4} x-2 \sin ^{2} x+1\) .
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Biến đổi
\(\begin{aligned}y=\ &\cos ^{4} x-2 \sin ^{2} x+1\\ =\ &\cos ^{4} x-2 \left(1-\cos^2 x\right)+1\\ =\ &\cos ^{4} x+2 \cos ^{2} x-1\\ =\ &\left(\cos^2 x+1\right)^2-2\end{aligned}\).
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& 0\leq \cos^2 x\leq 1\\ \Leftrightarrow\ & 1\leq \cos^2 x+1\leq 2\\ \Leftrightarrow\ &1\leq \left( \cos^2 x+1\right)^2\leq 4\\ \Leftrightarrow\ &-1\leq \left( \cos^2 x+1\right)^2-2\leq 2.\end{aligned}\)
Vậy \(\max\limits_{x \in \mathbb{R}} y=2\) khi \(x=0\) và \(\min\limits_{x \in \mathbb{R}} y=-1\) khi \(x=\displaystyle\frac{\pi}{2}\).
Bài tập 21
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{5-4 \sin x+\sin ^{2} x}\).
Xét hàm số \(g(x)=5-4 \sin x+\sin ^{2} x\) trên \(\mathbb{R}\).
Ta có
\(g(x)=5-4 \sin x+\sin ^{2} x\) \(=\left(\sin x -2\right)^2+1\)
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& & -1\leq \sin x\leq 1\\ \Leftrightarrow\ &-3\leq \sin x-2\leq -1\\ \Leftrightarrow\ &1\leq \left( \sin x-2\right)^2\leq 9\\ \Leftrightarrow\ &2\leq \left( \sin x-2\right)^2+1\leq 10.\end{aligned}\)
Suy ra:
\(2\leq g(x)\leq 10 \Rightarrow \sqrt{2}\leq y\leq \sqrt{10}\).
Vậy \(\max\limits_{x \in \mathbb{R}} y=\sqrt{10}\) khi \(x=-\displaystyle\frac{\pi}{2}\) và \(\min\limits_{x \in \mathbb{R}} y=\sqrt{2}\) khi \(x=\displaystyle\frac{\pi}{2}\).
Bài tập 22
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{\cos ^{2} x+6 \cos x+14}\) .
Xét hàm số \(g(x)=\cos ^{2} x+6 \cos x+14\) trên \(\mathbb{R}\).
Ta có
\(g(x)=\cos ^{2} x+6 \cos x+14\) \(=\left(\cos x +3\right)^2+5\)
Với mọi \(x\in \mathbb{R}\) ta có
\(\begin{aligned}& -1\leq \cos x\leq 1\\ \Leftrightarrow\ &2\leq \cos x+3\leq 4\\ \Leftrightarrow\ &4\leq \left( \cos x+3\right)^2\leq 16\\ \Leftrightarrow\ &9\leq \left( \cos x+3\right)^2+5\leq 21.\end{aligned}\)
Suy ra:
\(9\leq g(x)\leq 21 \Rightarrow 3\leq y\leq \sqrt{21}\).
Vậy \(\max\limits_{x \in \mathbb{R}} y=\sqrt{21}\) khi \(x=0\) và \(\min\limits_{x \in \mathbb{R}} y=3\) khi \(x=\pi\).
Bài tập 23
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=2(\sin x+\cos x)+\sin 2 x+3\).
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Đặt
\(t=\sin x+ \cos x=\sqrt{2}\sin \left(x+\displaystyle\frac{\pi}{4}\right)\), \(t\in \left[-\sqrt{2};\sqrt{2}\right]\).
Ta có
\(t^2=\left(\sin x+ \cos x\right)^2\) \(=1+2\sin x\cos x=1+\sin 2x\) \(\Rightarrow \sin 2x =t^2-1\).
Hàm số trở thành \(y=g(t)=t^2+2t+2\).
Bảng biến thiên của hàm số \(y=g(t)\) trên đoạn \( \left[-\sqrt{2};\sqrt{2}\right]\)

Vậy \(\max\limits_{x \in \mathbb{R}} y=4+2\sqrt{2}\) và \(\min\limits_{x \in \mathbb{R}} y=1\).
Bài tập 24
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin x+\cos x+2 \sin x \cos x-1\) .
Tập xác định \(\mathscr{D}=\mathbb{R}\).
Đặt \(t=\sin x+ \cos x=\sqrt{2}\sin \left(x+\displaystyle\frac{\pi}{4}\right)\), \(t\in \left[-\sqrt{2};\sqrt{2}\right]\).
Ta có
\(t^2=\left(\sin x+ \cos x\right)^2=1+2\sin x\cos x\) \(\Rightarrow 2\sin x\cos x =t^2-1\).
Hàm số trở thành \(y=g(t)=t^2+t-2\). \\
Bảng biến thiên của hàm số \(y=g(t)\) trên đoạn \( \left[-\sqrt{2};\sqrt{2}\right]\)

Vậy \(\max\limits_{x \in \mathbb{R}} y=\sqrt{2}\) và \(\min\limits_{x \in \mathbb{R}} y=-\displaystyle\frac{9}{4}\).
Bài tập 25
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=3-\sin 2 x\) trên đoạn \(\left[ 0; \displaystyle\frac{\pi}{2}\right]\)?
Ta có
\(x\in \left[ 0; \displaystyle\frac{\pi}{2}\right]\Rightarrow 2x\in \left[ 0; \pi\right]\).

Với mọi \(2x\in \left[ 0; \pi\right]\) ta có
\(\begin{aligned}& 0\leq \sin 2x\leq 1\\ \Leftrightarrow\ & -1\leq -\sin 2x\leq 0\\ \Leftrightarrow\ &2\leq 3-\sin 2x\leq 3.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[ 0; \tfrac{\pi}{2}\right]} y=3\) khi \(x=0\) và \(\min\limits_{x \in \left[ 0; \tfrac{\pi}{2}\right]} y=2\) khi \(x=\displaystyle\frac{\pi}{4}\).
Bài tập 26
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin 2 x+2\) trên \(\left[ 0; \displaystyle\frac{\pi}{2}\right]\)?
Ta có \(x\in \left[ 0; \displaystyle\frac{\pi}{2}\right]\Rightarrow 2x\in \left[ 0; \pi\right]\).

Với mọi \(2x\in \left[ 0; \pi\right]\) ta có
\(\begin{aligned}& 0\leq \sin 2x\leq 1\\ \Leftrightarrow\ &2\leq \sin 2x+2\leq 3.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[ 0; \tfrac{\pi}{2}\right]} y=3\) khi \(x=\displaystyle\frac{\pi}{4}\) và \(\min\limits_{x \in \left[ 0; \tfrac{\pi}{2}\right]} y=2\) khi \(x=0\).
Bài tập 27
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos \left(x+\displaystyle\frac{\pi}{3}\right)\) trên \([0 ; \pi]\).
Ta có
\(x\in \left[ 0; \pi\right]\) \(\Rightarrow x+\displaystyle\frac{\pi}{3}\in \left[ \displaystyle\frac{\pi}{3}; \displaystyle\frac{4\pi}{3}\right]\).

Do đó: \( -1 \leq \cos \left(x+\displaystyle\frac{\pi}{3}\right)\leq \displaystyle\frac{1}{2}\).
Vậy \(\max\limits_{x \in [0 ; \pi]} y=\displaystyle\frac{1}{2}\) khi \(x=0\) và \(\min\limits_{x \in [0 ; \pi]} y=-1\) khi \(x=\displaystyle\frac{2\pi}{3}\).
Bài tập 28
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin \left(2 x+\displaystyle\frac{\pi}{4}\right)+\displaystyle\frac{1}{2}\) trên \(\left[-\displaystyle\frac{\pi}{4} ; \displaystyle\frac{\pi}{4}\right]\).
Ta có \(x\in \left[ -\displaystyle\frac{\pi}{4}; \displaystyle\frac{\pi}{4}\right]\) \(\Rightarrow 2x+\displaystyle\frac{\pi}{4}\in \left[-\displaystyle\frac{\pi}{4}; \displaystyle\frac{3\pi}{4}\right]\).

Do đó:
\(\begin{aligned}& -\displaystyle\frac{\sqrt{2}}{2}\leq \sin \left(2 x+\displaystyle\frac{\pi}{4}\right)\leq 1\\ \Rightarrow\ & \displaystyle\frac{1-\sqrt{2}}{2}\leq \sin \left(2 x+\displaystyle\frac{\pi}{4}\right)+\displaystyle\frac{1}{2}\leq \displaystyle\frac{3}{2}.\end{aligned}\)
Vậy \(\max\limits_{x \in\left[-\tfrac{\pi}{4} ; \tfrac{\pi}{4}\right]} y=\displaystyle\frac{3}{2}\) và \(\min\limits_{x \in \left[-\tfrac{\pi}{4} ; \tfrac{\pi}{4}\right]} y=\displaystyle\frac{1-\sqrt{2}}{2}\).
Bài tập 29
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin^4 x+\cos^4 x-1\) = trên \(\left[0 ; \displaystyle\frac{\pi}{6}\right]\).
Ta có
\(\begin{aligned}&\sin^4 x+\cos^4 x\\ =\ & \left(\sin^2 x+\cos^2 x\right)^2-2\sin^2 x\cdot \cos^2 x\\ =\ &1-\displaystyle\frac{1}{2}\sin^2 2x\\ =\ &1-\displaystyle\frac{1-\cos 4x}{4}\\ =\ &\displaystyle\frac{3}{4}+\displaystyle\frac{1}{4}\cos 4x.\end{aligned}\)
Suy ra:
\(y=\sin^4 x+\cos^4 x-1=\displaystyle\frac{1}{4}\cos 4x-\displaystyle\frac{1}{4}\).

Do \(x\in \left[ 0 ; \displaystyle\frac{\pi}{6}\right]\Rightarrow 4x \in \left[0; \displaystyle\frac{2\pi}{3}\right]\).
Do đó:
\(\begin{aligned}& -\displaystyle\frac{1}{2}\leq\cos 4x \leq 1\\ \Leftrightarrow\ & -\displaystyle\frac{1}{8}\leq \displaystyle\frac{1}{4}\cos 4x \leq \displaystyle\frac{1}{4}\\ \Leftrightarrow\ & -\displaystyle\frac{3}{8}\leq \displaystyle\frac{1}{4}\cos 4x-\displaystyle\frac{1}{4} \leq 0.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[0 ; \tfrac{\pi}{6}\right]} y=0\) và \(\min\limits_{x \in \left[0 ; \tfrac{\pi}{6}\right]} y=-\displaystyle\frac{3}{8}\).
Bài tập 30
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin^6 x+\cos^6 x\) trên \(\left[-\displaystyle\frac{\pi}{2} ; \displaystyle\frac{\pi}{2}\right]\).
Ta có
\(\begin{aligned}&\sin^6 x+\cos^6 x\\ =\ & \left(\sin^2 x+\cos^2 x\right)^3-3\sin^2 x\cdot \cos^2 x\left(\sin^2 x+\cos^2 x \right)\\ =\ &1-\displaystyle\frac{3}{4}\sin^2 2x\\ =\ &1-\displaystyle\frac{3}{4}\cdot \displaystyle\frac{1-\cos 4x}{2}\\ =\ &\displaystyle\frac{5}{8}+\displaystyle\frac{3}{8}\cos 4x.\end{aligned}\)
Suy ra:
\(y=\sin^6 x+\cos^6 x = \displaystyle\frac{5}{8}+\displaystyle\frac{3}{8}\cos 4x\).
Do \(x\in \left[-\displaystyle\frac{\pi}{2} ; \displaystyle\frac{\pi}{2} \right]\Rightarrow 4x \in \left[-2\pi ; 2\pi\right]\) nên
\(\begin{aligned}& -1\leq\cos 4x \leq 1\\ \Leftrightarrow\ & -\displaystyle\frac{3}{8}\leq \displaystyle\frac{3}{8}\cos 4x \leq \displaystyle\frac{3}{8}\\ \Leftrightarrow\ & \displaystyle\frac{1}{4}\leq \displaystyle\frac{5}{8}+ \displaystyle\frac{3}{8}\cos 4x \leq 1.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[-\tfrac{\pi}{2} ; \tfrac{\pi}{2}\right]} y=1\) và \(\min\limits_{x \in \left[-\tfrac{\pi}{2} ; \tfrac{\pi}{2}\right]} y=\displaystyle\frac{1}{4}\).
Bài tập 31
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{3} \sin 2 x+2 \cos^2 x+3\) trên \(\left[-\displaystyle\frac{5 \pi}{6}; \displaystyle\frac{\pi}{4}\right]\).
Ta có
\(\begin{aligned}y=\ & \sqrt{3} \sin 2 x+2 \cos^2 x+3\\ =\ &\sqrt{3} \sin 2 x+2\cdot\displaystyle\frac{1+\cos 2x}{2}+3\\ =\ & \sqrt{3} \sin 2 x+\cos 2x+4\\ =\ &2\sin \left(2x+\displaystyle\frac{\pi}{6}\right)+4.\end{aligned}\)
Do \(x\in \left[-\displaystyle\frac{5 \pi}{6}; \displaystyle\frac{\pi}{4}\right]\) \(\Rightarrow 2x \in \left[-\displaystyle\frac{5 \pi}{3}; \displaystyle\frac{\pi}{2}\right]\) \(\Rightarrow 2x +\displaystyle\frac{\pi}{6}\in \left[-\displaystyle\frac{3\pi}{2}; \displaystyle\frac{2\pi}{3}\right]\) .
Do đó:
\(\begin{aligned}& -1\leq \sin \left(2x+\displaystyle\frac{\pi}{6}\right) \leq 1\\ \Leftrightarrow\ & -2\leq 2\sin \left(2x+\displaystyle\frac{\pi}{6}\right) \leq 2\\ \Leftrightarrow\ & 2\leq 2\sin \left(2x+\displaystyle\frac{\pi}{6}\right)+4 \leq 6.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[-\tfrac{5 \pi}{6}; \tfrac{\pi}{4}\right]} y=6\) và \(\min\limits_{x \in \left[-\tfrac{5 \pi}{6}; \tfrac{\pi}{4}\right]} y=2\).
Bài tập 32
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin 2 x+\cos 2 x+3\) trên \(\left[-\displaystyle\frac{\pi}{4} ; \displaystyle\frac{\pi}{4}\right]\).
Ta có \(y= \sin 2 x+\cos 2 x+3= \sqrt{2}\sin \left(2x+\displaystyle\frac{\pi}{4}\right)+3\).
Do \(x\in \left[-\displaystyle\frac{\pi}{4} ; \displaystyle\frac{\pi}{4}\right]\Rightarrow 2x \in \left[-\displaystyle\frac{\pi}{2} ; \displaystyle\frac{\pi}{2}\right]\) \(\Rightarrow 2x +\displaystyle\frac{\pi}{4}\in \left[-\displaystyle\frac{\pi}{4}; \displaystyle\frac{3\pi}{4}\right]\).

Do đó:
\(\begin{aligned}& -\displaystyle\frac{\sqrt{2}}{2}\leq\sin \left(2x+\displaystyle\frac{\pi}{4}\right) \leq 1\\ \Leftrightarrow\ & -1\leq \sqrt{2} \sin \left(2x+\displaystyle\frac{\pi}{4}\right)\leq \sqrt{2}\\ \Leftrightarrow\ & 2\leq \sqrt{2}\sin \left(2x+\displaystyle\frac{\pi}{4}\right)+3 \leq 3+\sqrt{2}.\end{aligned}\)
Vậy \(\max\limits_{x \in \left[-\tfrac{\pi}{4} ; \tfrac{\pi}{4}\right]} y=3+\sqrt{2}\) và \(\min\limits_{x \in \left[-\tfrac{\pi}{4} ; \tfrac{\pi}{4}\right]} y=2\).
Dạng 3. Xét tính chẵn lẻ của hàm số lượng giác
Phương pháp giải
Bài tập 1
Xét tính chẵn, lẻ của hàm số \(f(x)=\sin^2 2x+\cos 3x\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\sin^2(-2x)+\cos(-3x)\) \(=\sin^2 2x+\cos 3x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 2
Xét tính chẵn, lẻ của hàm số \(f(x)=\cos^2 3x+\cos x\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\cos^2(-3x)+\cos(-x)\) \(=\cos^2 3x+\cos x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 3
Xét tính chẵn, lẻ của hàm số \(f(x)=\displaystyle\frac{\sin^2 x-\cos x}{\sin 3x}\).
Điều kiện xác định \(\sin 3x\ne0\Leftrightarrow x\ne\displaystyle\frac{k\pi}{3}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{3},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\displaystyle\frac{\sin^2(-x)-\cos(-x)}{\sin(-3x)}\) \(=\displaystyle\frac{\sin^2 x-\cos x}{-\sin 3x}=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Bài tập 4
Xét tính chẵn, lẻ của hàm số \(f(x)=1+\cos x\cdot\sin\left(\displaystyle\frac{3\pi}{2}-2x\right)\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(x)=1+\cos x\cdot\sin\left(\displaystyle\frac{3\pi}{2}-2x\right)\) \(=1-\cos x\cdot\sin\left(\displaystyle\frac{\pi}{2}-2x\right)\) \(=1-\cos x\cdot\cos 2x\).
Khi đó
\(f(-x)=1-\cos(-x)\cdot\cos(-2x)\) \(=1-\cos x\cdot\cos 2x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 5
Xét tính chẵn, lẻ của hàm số \(f(x)=\cos\sqrt{x^2-16}\).
Điều kiện xác định của hàm số là \(x^2-16\ge0\Leftrightarrow\left[\begin{aligned}x\ge4\\ x\le-4.\end{aligned}\right.\)
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus(-4;4)\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\cos\sqrt{(-x)^2-16}\) \(=\cos\sqrt{x^2-16}=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 6
Xét tính chẵn, lẻ của hàm số \(f(x)=\tan x+\cot x\).
Điều kiện xác định của hàm số là \(\begin{cases}\sin x\ne0\\ \cos x\ne0\end{cases}\Leftrightarrow x\ne\displaystyle\frac{k\pi}{2}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{2},\ k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\tan(-x)+\cot(-x)\) \(=-\tan x-\cot x=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Bài tập 7
Xét tính chẵn, lẻ của hàm số \(f(x)=\cot(4x+5\pi)\cdot\tan(2x-3\pi)\).
Ta có
\(f(x)=\cot(4x+5\pi)\cdot\tan(2x-3\pi)\) \(=\cot 4x\cdot\tan 2x\).
Điều kiện xác định của hàm số là
\(\begin{cases}\sin 4x\ne0\\ \cos 2x\ne0\end{cases}\) \(\Leftrightarrow\begin{cases}x\ne\displaystyle\frac{k\pi}{4}\\ x\ne\displaystyle\frac{\pi}{4}+\displaystyle\frac{k\pi}{2}\end{cases}\) \(\Leftrightarrow x\ne\displaystyle\frac{k\pi}{4}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{4},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\cot(-4x)\cdot\tan(-2x)\) \(=\cot 4x\cdot\tan 2x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 8
Xét tính chẵn, lẻ của hàm số \(f(x)=\sin^3(3x+\pi)+\cot(2x-7\pi)\).
Ta có
\(f(x)=\sin^3(3x+\pi)+\cot(2x-7\pi)\) \(=-\sin^3 x+\cot 2x\).
Điều kiện xác định của hàm số là \(\sin 2x\ne0\Leftrightarrow x\ne\displaystyle\frac{k\pi}{2}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{2},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=-\sin^3(-x)+\cot(-2x)\) \(=\sin^3 x-\cot 2x=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Bài tập 9
Xét tính chẵn, lẻ của hàm số \(f(x)=\left|\sin x-\displaystyle\frac{1}{2}\right|+\left|\sin x+\displaystyle\frac{1}{2}\right|\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng. Ta có
\(\begin{aligned}f(-x)=\ &\left|\sin (-x)-\displaystyle\frac{1}{2}\right|+\left|\sin (-x)+\displaystyle\frac{1}{2}\right|\\ =\ &\left|-\sin x-\displaystyle\frac{1}{2}\right|+\left|-\sin x+\displaystyle\frac{1}{2}\right|\\ =\ &\left|\sin x+\displaystyle\frac{1}{2}\right|+\left|\sin x-\displaystyle\frac{1}{2}\right|\\ =\ &f(x),\,\forall x\in\mathscr{D}.\end{aligned}\)
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 10
Xét tính chẵn, lẻ của hàm số \(f(x)=\displaystyle\frac{\sqrt{\cos x+2}+\cot^2 x}{\sin 4x}\).
Điều kiện xác định
\(\begin{cases}\cos x+2\ge 0\\ \sin x\ne 0\\ \sin 4x\ne 0\end{cases}\) \(\Leftrightarrow\begin{cases}\cos x\ge -2\\ \sin 4x\ne 0\end{cases}\) \(\Leftrightarrow 4x\ne k\pi\) \(\Leftrightarrow x\ne\displaystyle\frac{k\pi}{4}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{4},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\displaystyle\frac{\sqrt{\cos(-x)+2}+\cot^2(-x)}{\sin(-4x)}\) \(=\displaystyle\frac{\sqrt{\cos x+2}+\cot^2 x}{-\sin 4x}=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Dạng 4. Tìm chu kì của hàm số lượng giác
Phương pháp giải
Bài tập 1
Hàm số \(y=\sin 2x\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=2\pi\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=\pi\)
D. \(T_0=4\pi\)
Ta có hàm số \(y=\sin 2x\) tuần hoàn với chu kỳ \(T_0=\displaystyle\frac{2\pi}{2}=\pi\).
Bài tập 2
Hàm số \(y=\tan 2x\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=\displaystyle\frac{\pi}{3}\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=2\pi\)
D. \(T_0=\pi\)
Ta có hàm số \(y=\tan 2x\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{\pi}{2}\).
Bài tập 3
Hàm số \(y=3\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=0\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=2\pi\)
D. \(T_0=4\pi\)
Ta có hàm số \(y=3\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{2\pi}{\tfrac{1}{2}}=4\pi\).
Bài tập 4
Hàm số \(f(x)=\sin\displaystyle\frac{x}{2}+2\cos\displaystyle\frac{3x}{2}\) tuần hoàn với chu kỳ chu kỳ là
A. \(5\pi\)
B. \(\displaystyle\frac{\pi}{2}\)
C. \(3\pi\)
D. \(4\pi\)
Ta có
+) hàm số \(\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ \(T_1=\displaystyle\frac{2\pi}{\tfrac{1}{2}}=4\pi\),
+) hàm số \(\cos\displaystyle\frac{3x}{2}\) tuần hoàn với chu kỳ \(T_2=\displaystyle\frac{2\pi}{\tfrac{3}{2}}=\displaystyle\frac{4\pi}{3}\).
Do đó hàm số \(f(x)\) tuần hoàn với chu kỳ \(T_0\) là bội chung nhỏ nhất của \(T_1\) và \(T_2\).
Do \(T_1\) là bội của \(T_2\) \(\left(\displaystyle\frac{T_1}{T_2}=3\right)\) nên \(T_0=T_1\).
Vậy hàm số \(f(x)\) đã cho tuần hoàn với chu kỳ \(T_0=4\pi\).
Bài tập 5
Tìm \(m\) để hàm số \(y=\cos mx\) tuần hoàn với chu kỳ \(T_0=\pi\).
A. \(m=\pm1\)
B. \(m=\pm2\)
C. \(m=\pm\displaystyle\frac{\pi}{2}\)
D. \(m=\pm\pi\)
Ta có hàm số \(y=\cos mx\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{2\pi}{|m|}\).
Để hàm số tuần hoàn với chu kỳ \(T_0=\pi\) thì
\(T=T_0\Leftrightarrow \displaystyle\frac{2\pi}{|m|}=\pi\Leftrightarrow |m|=2\Leftrightarrow m=\pm2\).
Bài tập 1
Xét tính chẵn, lẻ của hàm số \(f(x)=\sin^2 2x+\cos 3x\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\sin^2(-2x)+\cos(-3x)\) \(=\sin^2 2x+\cos 3x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 2
Xét tính chẵn, lẻ của hàm số \(f(x)=\cos^2 3x+\cos x\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\cos^2(-3x)+\cos(-x)\) \(=\cos^2 3x+\cos x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 3
Xét tính chẵn, lẻ của hàm số \(f(x)=\displaystyle\frac{\sin^2 x-\cos x}{\sin 3x}\).
Điều kiện xác định \(\sin 3x\ne0\Leftrightarrow x\ne\displaystyle\frac{k\pi}{3}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{3},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\displaystyle\frac{\sin^2(-x)-\cos(-x)}{\sin(-3x)}\) \(=\displaystyle\frac{\sin^2 x-\cos x}{-\sin 3x}=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Bài tập 4
Xét tính chẵn, lẻ của hàm số \(f(x)=1+\cos x\cdot\sin\left(\displaystyle\frac{3\pi}{2}-2x\right)\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(x)=1+\cos x\cdot\sin\left(\displaystyle\frac{3\pi}{2}-2x\right)\) \(=1-\cos x\cdot\sin\left(\displaystyle\frac{\pi}{2}-2x\right)\) \(=1-\cos x\cdot\cos 2x\).
Khi đó
\(f(-x)=1-\cos(-x)\cdot\cos(-2x)\) \(=1-\cos x\cdot\cos 2x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 5
Xét tính chẵn, lẻ của hàm số \(f(x)=\cos\sqrt{x^2-16}\).
Điều kiện xác định của hàm số là \(x^2-16\ge0\Leftrightarrow\left[\begin{aligned}x\ge4\\ x\le-4.\end{aligned}\right.\)
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus(-4;4)\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\cos\sqrt{(-x)^2-16}\) \(=\cos\sqrt{x^2-16}=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 6
Xét tính chẵn, lẻ của hàm số \(f(x)=\tan x+\cot x\).
Điều kiện xác định của hàm số là \(\begin{cases}\sin x\ne0\\ \cos x\ne0\end{cases}\Leftrightarrow x\ne\displaystyle\frac{k\pi}{2}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{2},\ k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\tan(-x)+\cot(-x)\) \(=-\tan x-\cot x=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Bài tập 7
Xét tính chẵn, lẻ của hàm số \(f(x)=\cot(4x+5\pi)\cdot\tan(2x-3\pi)\).
Ta có
\(f(x)=\cot(4x+5\pi)\cdot\tan(2x-3\pi)\) \(=\cot 4x\cdot\tan 2x\).
Điều kiện xác định của hàm số là
\(\begin{cases}\sin 4x\ne0\\ \cos 2x\ne0\end{cases}\) \(\Leftrightarrow\begin{cases}x\ne\displaystyle\frac{k\pi}{4}\\ x\ne\displaystyle\frac{\pi}{4}+\displaystyle\frac{k\pi}{2}\end{cases}\) \(\Leftrightarrow x\ne\displaystyle\frac{k\pi}{4}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{4},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\cot(-4x)\cdot\tan(-2x)\) \(=\cot 4x\cdot\tan 2x=f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 8
Xét tính chẵn, lẻ của hàm số \(f(x)=\sin^3(3x+\pi)+\cot(2x-7\pi)\).
Ta có
\(f(x)=\sin^3(3x+\pi)+\cot(2x-7\pi)\) \(=-\sin^3 x+\cot 2x\).
Điều kiện xác định của hàm số là \(\sin 2x\ne0\Leftrightarrow x\ne\displaystyle\frac{k\pi}{2}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{2},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=-\sin^3(-x)+\cot(-2x)\) \(=\sin^3 x-\cot 2x=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Bài tập 9
Xét tính chẵn, lẻ của hàm số \(f(x)=\left|\sin x-\displaystyle\frac{1}{2}\right|+\left|\sin x+\displaystyle\frac{1}{2}\right|\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng. Ta có
\(\begin{aligned}f(-x)=\ &\left|\sin (-x)-\displaystyle\frac{1}{2}\right|+\left|\sin (-x)+\displaystyle\frac{1}{2}\right|\\ =\ &\left|-\sin x-\displaystyle\frac{1}{2}\right|+\left|-\sin x+\displaystyle\frac{1}{2}\right|\\ =\ &\left|\sin x+\displaystyle\frac{1}{2}\right|+\left|\sin x-\displaystyle\frac{1}{2}\right|\\ =\ &f(x),\,\forall x\in\mathscr{D}.\end{aligned}\)
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
Bài tập 10
Xét tính chẵn, lẻ của hàm số \(f(x)=\displaystyle\frac{\sqrt{\cos x+2}+\cot^2 x}{\sin 4x}\).
Điều kiện xác định
\(\begin{cases}\cos x+2\ge 0\\ \sin x\ne 0\\ \sin 4x\ne 0\end{cases}\) \(\Leftrightarrow\begin{cases}\cos x\ge -2\\ \sin 4x\ne 0\end{cases}\) \(\Leftrightarrow 4x\ne k\pi\) \(\Leftrightarrow x\ne\displaystyle\frac{k\pi}{4}\), \(k\in\mathbb{Z}\).
Tập xác định của hàm số \(\mathscr{D}=\mathbb{R}\setminus\left\{\displaystyle\frac{k\pi}{4},\,k\in\mathbb{Z}\right\}\).
Với mọi \(x\in\mathscr{D}\) thì \(-x\in\mathscr{D}\) nên \(\mathscr{D}\) là tập đối xứng.
Ta có
\(f(-x)=\displaystyle\frac{\sqrt{\cos(-x)+2}+\cot^2(-x)}{\sin(-4x)}\) \(=\displaystyle\frac{\sqrt{\cos x+2}+\cot^2 x}{-\sin 4x}=-f(x)\), \(\forall x\in\mathscr{D}\).
Do đó hàm số \(f(x)\) đã cho là hàm số lẻ.
Dạng 4. Tìm chu kì của hàm số lượng giác
Phương pháp giải
Bài tập 1
Hàm số \(y=\sin 2x\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=2\pi\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=\pi\)
D. \(T_0=4\pi\)
Ta có hàm số \(y=\sin 2x\) tuần hoàn với chu kỳ \(T_0=\displaystyle\frac{2\pi}{2}=\pi\).
Bài tập 2
Hàm số \(y=\tan 2x\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=\displaystyle\frac{\pi}{3}\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=2\pi\)
D. \(T_0=\pi\)
Ta có hàm số \(y=\tan 2x\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{\pi}{2}\).
Bài tập 3
Hàm số \(y=3\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=0\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=2\pi\)
D. \(T_0=4\pi\)
Ta có hàm số \(y=3\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{2\pi}{\tfrac{1}{2}}=4\pi\).
Bài tập 4
Hàm số \(f(x)=\sin\displaystyle\frac{x}{2}+2\cos\displaystyle\frac{3x}{2}\) tuần hoàn với chu kỳ chu kỳ là
A. \(5\pi\)
B. \(\displaystyle\frac{\pi}{2}\)
C. \(3\pi\)
D. \(4\pi\)
Ta có
+) hàm số \(\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ \(T_1=\displaystyle\frac{2\pi}{\tfrac{1}{2}}=4\pi\),
+) hàm số \(\cos\displaystyle\frac{3x}{2}\) tuần hoàn với chu kỳ \(T_2=\displaystyle\frac{2\pi}{\tfrac{3}{2}}=\displaystyle\frac{4\pi}{3}\).
Do đó hàm số \(f(x)\) tuần hoàn với chu kỳ \(T_0\) là bội chung nhỏ nhất của \(T_1\) và \(T_2\).
Do \(T_1\) là bội của \(T_2\) \(\left(\displaystyle\frac{T_1}{T_2}=3\right)\) nên \(T_0=T_1\).
Vậy hàm số \(f(x)\) đã cho tuần hoàn với chu kỳ \(T_0=4\pi\).
Bài tập 5
Tìm \(m\) để hàm số \(y=\cos mx\) tuần hoàn với chu kỳ \(T_0=\pi\).
A. \(m=\pm1\)
B. \(m=\pm2\)
C. \(m=\pm\displaystyle\frac{\pi}{2}\)
D. \(m=\pm\pi\)
Ta có hàm số \(y=\cos mx\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{2\pi}{|m|}\).
Để hàm số tuần hoàn với chu kỳ \(T_0=\pi\) thì
\(T=T_0\Leftrightarrow \displaystyle\frac{2\pi}{|m|}=\pi\Leftrightarrow |m|=2\Leftrightarrow m=\pm2\).
Bài tập 1
Hàm số \(y=\sin 2x\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=2\pi\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=\pi\)
D. \(T_0=4\pi\)
Ta có hàm số \(y=\sin 2x\) tuần hoàn với chu kỳ \(T_0=\displaystyle\frac{2\pi}{2}=\pi\).
Bài tập 2
Hàm số \(y=\tan 2x\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=\displaystyle\frac{\pi}{3}\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=2\pi\)
D. \(T_0=\pi\)
Ta có hàm số \(y=\tan 2x\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{\pi}{2}\).
Bài tập 3
Hàm số \(y=3\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ chu kỳ là
A. \(T_0=0\)
B. \(T_0=\displaystyle\frac{\pi}{2}\)
C. \(T_0=2\pi\)
D. \(T_0=4\pi\)
Ta có hàm số \(y=3\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{2\pi}{\tfrac{1}{2}}=4\pi\).
Bài tập 4
Hàm số \(f(x)=\sin\displaystyle\frac{x}{2}+2\cos\displaystyle\frac{3x}{2}\) tuần hoàn với chu kỳ chu kỳ là
A. \(5\pi\)
B. \(\displaystyle\frac{\pi}{2}\)
C. \(3\pi\)
D. \(4\pi\)
Ta có
+) hàm số \(\sin\displaystyle\frac{x}{2}\) tuần hoàn với chu kỳ \(T_1=\displaystyle\frac{2\pi}{\tfrac{1}{2}}=4\pi\),
+) hàm số \(\cos\displaystyle\frac{3x}{2}\) tuần hoàn với chu kỳ \(T_2=\displaystyle\frac{2\pi}{\tfrac{3}{2}}=\displaystyle\frac{4\pi}{3}\).
Do đó hàm số \(f(x)\) tuần hoàn với chu kỳ \(T_0\) là bội chung nhỏ nhất của \(T_1\) và \(T_2\).
Do \(T_1\) là bội của \(T_2\) \(\left(\displaystyle\frac{T_1}{T_2}=3\right)\) nên \(T_0=T_1\).
Vậy hàm số \(f(x)\) đã cho tuần hoàn với chu kỳ \(T_0=4\pi\).
Bài tập 5
Tìm \(m\) để hàm số \(y=\cos mx\) tuần hoàn với chu kỳ \(T_0=\pi\).
A. \(m=\pm1\)
B. \(m=\pm2\)
C. \(m=\pm\displaystyle\frac{\pi}{2}\)
D. \(m=\pm\pi\)
Ta có hàm số \(y=\cos mx\) tuần hoàn với chu kỳ \(T=\displaystyle\frac{2\pi}{|m|}\).
Để hàm số tuần hoàn với chu kỳ \(T_0=\pi\) thì
\(T=T_0\Leftrightarrow \displaystyle\frac{2\pi}{|m|}=\pi\Leftrightarrow |m|=2\Leftrightarrow m=\pm2\).